Advertisements
Advertisements
प्रश्न
Find the smallest number by which the given number must be divided so that the resulting number is a perfect square:
14283
उत्तर
For each question, factorise the number into its prime factors.
14283 = 3 x 3 x 3 x 23 x 23
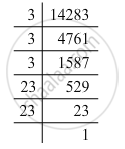
Grouping the factors into pairs:
14283 = (3 x 3) x (23 x 23) x 3
Here, the factor 3 does not occur in pairs. To be a perfect square, all the factors have to be in pairs. Hence, the smallest number by which 14283 must be divided for it to be a perfect square is 3.
APPEARS IN
संबंधित प्रश्न
Find the square root of the following number by the prime factorisation method.
9604
For the following number, find the smallest whole number by which it should be divided so as to get a perfect square number. Also find the square root of the square number so obtained.
1620
Find the smallest number by which 1152 must be divided so that it becomes a perfect square. Also, find the square root of the number so obtained.
The product of two numbers is 1296. If one number is 16 times the other, find the numbers.
Find the least square number, exactly divisible by each one of the numbers:
(i) 6, 9, 15 and 20
Write the prime factorization of the following number and hence find their square root.
9604
By splitting into prime factors, find the square root of 396900.
Show that 500 is not a perfect square.
Using prime factorisation, find the square roots of 11025
Using prime factorisation, find the square roots of 4761
