Advertisements
Advertisements
Question
Find the square of the following number:
451
Solution
We will use visual method as it is the most efficient method to solve this problem.
We have:
451 = 450 + 1
Hence, let us draw a square having side 451 units. Let us split it into 450 units and 1 units.
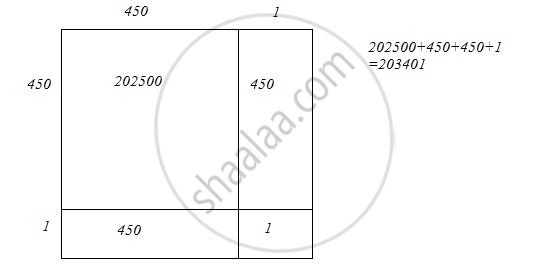
Hence, the square of 451 is 203401.
APPEARS IN
RELATED QUESTIONS
Find the square of the given number.
46
What will be the units digit of the square of the following number?
55555
Observe the following pattern
22 − 12 = 2 + 1
32 − 22 = 3 + 2
42 − 32 = 4 + 3
52 − 42 = 5 + 4
and find the value of
992 − 962
Observe the following pattern \[1 = \frac{1}{2}\left\{ 1 \times \left( 1 + 1 \right) \right\}\]
\[ 1 + 2 = \frac{1}{2}\left\{ 2 \times \left( 2 + 1 \right) \right\}\]
\[ 1 + 2 + 3 = \frac{1}{2}\left\{ 3 \times \left( 3 + 1 \right) \right\}\]
\[1 + 2 + 3 + 4 = \frac{1}{2}\left\{ 4 \times \left( 4 + 1 \right) \right\}\]and find the values of following:
31 + 32 + ... + 50
Observe the following pattern \[1^2 = \frac{1}{6}\left[ 1 \times \left( 1 + 1 \right) \times \left( 2 \times 1 + 1 \right) \right]\]
\[ 1^2 + 2^2 = \frac{1}{6}\left[ 2 \times \left( 2 + 1 \right) \times \left( 2 \times 2 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 = \frac{1}{6}\left[ 3 \times \left( 3 + 1 \right) \times \left( 2 \times 3 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 + 4^2 = \frac{1}{6}\left[ 4 \times \left( 4 + 1 \right) \times \left( 2 \times 4 + 1 \right) \right]\] and find the values :
12 + 22 + 32 + 42 + ... + 102
Observe the following pattern \[1^2 = \frac{1}{6}\left[ 1 \times \left( 1 + 1 \right) \times \left( 2 \times 1 + 1 \right) \right]\]
\[ 1^2 + 2^2 = \frac{1}{6}\left[ 2 \times \left( 2 + 1 \right) \times \left( 2 \times 2 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 = \frac{1}{6}\left[ 3 \times \left( 3 + 1 \right) \times \left( 2 \times 3 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 + 4^2 = \frac{1}{6}\left[ 4 \times \left( 4 + 1 \right) \times \left( 2 \times 4 + 1 \right) \right]\] and find the values :
52 + 62 + 72 + 82 + 92 + 102 + 112 + 122
Find the square of the following number:
265
Find the square of the following number:
512
For every natural number m, (2m – 1, 2m2 – 2m, 2m2 – 2m + 1) is a pythagorean triplet.
A 5.5 m long ladder is leaned against a wall. The ladder reaches the wall to a height of 4.4 m. Find the distance between the wall and the foot of the ladder.
