Advertisements
Advertisements
Question
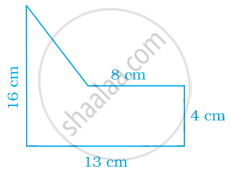
Find the area enclosed by the following figure:
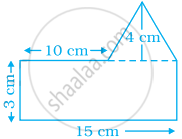
Solution
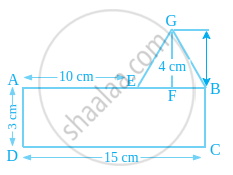
The given shape contains a rectangle and a triangle.
For rectangle, l = 15 m and b = 3 cm
∴ Area of rectangle = l × b = 15 × 3 = 45 cm2
According to the figure,
BE = AB – AE = 15 – 10 = 5 cm
For triangle, base (b) = BE = 5 cm and height (h) = 4 cm
∴ Area of ΔBEG = `1/2` × b × h = `1/2` × 5 × 4 = 10 cm2
∴ Total area enclosed by the shape = (45 + 10) cm2 = 55 cm2.
APPEARS IN
RELATED QUESTIONS
A 3 m wide path runs outside and around a rectangular park of length 125 m and breadth 65 m. Find the area of the path.
A picture is painted on a cardboard 8 cm long and 5 cm wide such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
A verandah of width 2.25 m is constructed all along outside a room which is 5.5 m long and 4 m wide. Find:
1) the area of the verandah
2) the cost of cementing the floor of the verandah at the rate of Rs 200 per m2.
Through a rectangular field of length 90 m and breadth 60 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the fields. If the width of each road is 3 m, find
1)the area covered by the roads.
2) the cost of constructing the roads at the rate of Rs 110 per m2.
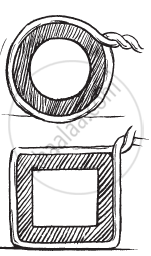
Pragya wrapped a cord around a circular pipe of radius 4 cm (adjoining figure) and cut off the length required of the cord. Then she wrapped it around a square box of side 4 cm (also shown). Did she have any cord left? (π= 3.14)
In the following figure, find the area of the shaded portions
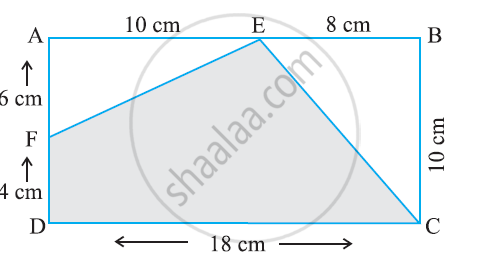
In the following figure, find the area of the shaded portions
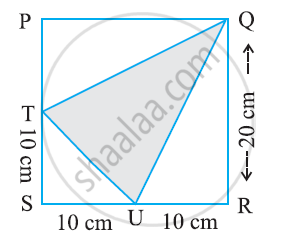
A path 5 m wide runs along inside a square park of side 100 m. Find the area of the path. Also, find the cost of cementing it at the rate of Rs. 250 per 10 m2.
Two crossroads, each of width 5 m, run at right angles through the center of a rectangular park of length 70 m and breadth 45 m and parallel to its sides. Find the area of the roads. Also, find the cost of constructing the roads at a rate of Rs. 105 per m2.
Find the area enclosed by the following figure: