Advertisements
Advertisements
Question
Find the capacity of a cylindrical container with an internal diameter of 28 cm and a height of 20 cm.
Solution
Diameter = 28 cm
Radius = `28/2` cm = 14 cm
Height = 20 cm
Volume = πr2h = `22/7` x 14 x 14 x 20
Volume = 12320 cm3
APPEARS IN
RELATED QUESTIONS
The floor of a rectangular hall has a perimeter 250 m. If the cost of panting the four walls at the rate of Rs.10 per m2 is Rs.15000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area.]
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost ofcovering it with sheet of paper at the rates of Rs. 8 and Rs. 9.50 per m2 is Rs.1248. Find the dimensions of the box.
Find the height of a cuboid of volume 100 cm3, whose length and breadth are 5 cm and 4 cm respectively.
A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it, beads of volume 1.5 cm3 each are to be made. Find the number of beads that can be made from the block.
The weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
How many soap cakes can be placed in a box of size 56 cm × 0.4 m × 0.25 m, if the size of a soap cake is 7 cm × 5 cm × 2.5 cm?
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions islength = 4 m, breadth = 2.5 m, height = 50 cm.
Find the surface area of a cuboid whose length = 10 cm, breadth = 12 cm, height = 14 cm.
If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that \[\frac{1}{V} = \frac{2}{S}\left( \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \right)\]
The cost of preparing the walls of a room 12 m long at the rate of Rs 1.35 per square metre is Rs 340.20 and the cost of matting the floor at 85 paise per square metre is Rs 91.80. Find the height of the room.
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with sheet of paper at the rates of Rs 8 and Rs 9.50 per m2 is Rs. 1248. Find the dimensions of the box.
The length, breadth, and height of a rectangular solid are in the ratio 5: 4: 2. If the total surface area is 1216 cm2, find the length, the breadth, and the height of the solid.
The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m3; find its length.
Find the length of each edge of a cube, if its volume is :
(i) 216 cm3
(ii) 1.728 m3
The dimension of a class-room are; length = 15 m, breadth = 12 m and height = 7.5 m. Find, how many children can be accommodated in this class-room; assuming 3.6 m3 of air is needed for each child.
The internal length, breadth, and height of a closed box are 1 m, 80 cm, and 25 cm. respectively. If its sides are made of 2.5 cm thick wood; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
The total surface area of a cylinder is 6512 cm2 and the circumference of its bases is 88 cm. Find:
(i) its radius
(ii) its volume
In a building, there are 24 cylindrical pillars. For each pillar, the radius is 28 m, and the height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m2.
The length, breadth, and height of a rectangular solid are in the ratio 6 : 4 :3. If the total surface area is 1728 cm2. Find its dimensions.
375 persons can be accommodated in a room whose dimensions are in the ratio of 6 : 4 : 1. Calculate the area of the four walls of the room if the each person consumes 64m3 of air.
Find the volume of wood used in making a closed box 22 cm by 18 cm by 14 cm, using a 1 cm thick wood. Also, find the cost of wood required to make the box at the rate of Rs. 5 per cm³ How many cubes of side 2 cm can be placed in the box?
Two cuboids with equal volumes will always have equal surface areas.
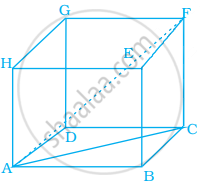
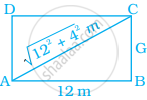
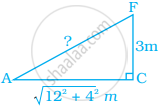
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side. Find the volume and the whole surface area of the solid thus generated.
