Advertisements
Advertisements
Question
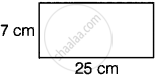
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side. Find the volume and the whole surface area of the solid thus generated.
Solution
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side which make a cylinder with base 25 cm and height 7 cm.
Surface area of a base = 2πr
∴ 2πr = 25 cm
⇒ `r = (25 xx 7)/(2 xx 22) = 175/44 cm`
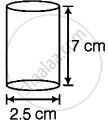
Volume of a cylinder = πr2h
= `22/7 xx 175/44 xx 175/44 xx 7`
= `(175 xx 175)/(2 xx 44)`
= `30625/88`
= 348.011 cm3
Surface area = 2πrh
= `2 xx 22/7 xx 175/44 xx 7`
= `44/44 xx 175`
= 175 cm2
APPEARS IN
RELATED QUESTIONS
The floor of a rectangular hall has a perimeter 250 m. If the cost of panting the four walls at the rate of Rs.10 per m2 is Rs.15000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area.]
Find the weight of solid rectangular iron piece of size 50 cm × 40 cm × 10cm, if 1 cm3 of iron weighs 8 gm.
A cuboidal box is 5 cm by 5 cm by 4 cm. Find its surface area.
10 cubic metres clay is uniformly spread on a land of area 10 ares. the rise in the level of the ground is
If A1, A2, and A3 denote the areas of three adjacent faces of a cuboid, then its volume is
The volume of a cuboid is 3456 cm3. If its length = 24 cm and breadth = 18 cm ; find its height.
The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m3; find its length.
Find the volume and total surface area of a cube whose each edge is:
(i) 8 cm
(ii) 2 m 40 cm.
A solid cuboid of metal has dimensions 24 cm, 18 cm, and 4 cm. Find its volume.
A tank 30 m long, 24 m wide, and 4.5 m deep is to be made. It is open from the top. Find the cost of iron-sheet required, at the rate of ₹ 65 per m2, to make the tank.
