Advertisements
Advertisements
प्रश्न
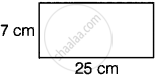
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side. Find the volume and the whole surface area of the solid thus generated.
Advertisements
उत्तर
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side which make a cylinder with base 25 cm and height 7 cm.
Surface area of a base = 2πr
∴ 2πr = 25 cm
⇒ `r = (25 xx 7)/(2 xx 22) = 175/44 cm`
Volume of a cylinder = πr2h
= `22/7 xx 175/44 xx 175/44 xx 7`
= `(175 xx 175)/(2 xx 44)`
= `30625/88`
= 348.011 cm3
Surface area = 2πrh
= `2 xx 22/7 xx 175/44 xx 7`
= `44/44 xx 175`
= 175 cm2
APPEARS IN
संबंधित प्रश्न
Find the weight of solid rectangular iron piece of size 50 cm × 40 cm × 10cm, if 1 cm3 of iron weighs 8 gm.
A cuboid has total surface area of 372 cm2 and its lateral surface area is 180 cm2, find the area of its base.
If each edge of a cube is increased by 50%, the percentage increase in its surface area is
The length, breadth, and height of a cuboid are in the ratio 5 : 3: 2. If its volume is 240 cm3; find its dimensions. Also, find the total surface area of the cuboid.
The total surface area of a cylinder is 6512 cm2 and the circumference of its bases is 88 cm. Find:
(i) its radius
(ii) its volume
Three equal cubes of sides 5cm each are placed to form a cuboid. Find the volume and the total surface area of the cuboid.
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.
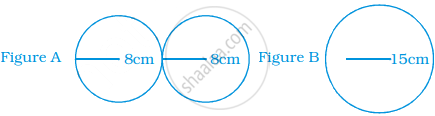
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?
