Advertisements
Advertisements
प्रश्न
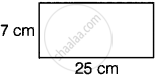
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side. Find the volume and the whole surface area of the solid thus generated.
उत्तर
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side which make a cylinder with base 25 cm and height 7 cm.
Surface area of a base = 2πr
∴ 2πr = 25 cm
⇒ `r = (25 xx 7)/(2 xx 22) = 175/44 cm`
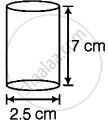
Volume of a cylinder = πr2h
= `22/7 xx 175/44 xx 175/44 xx 7`
= `(175 xx 175)/(2 xx 44)`
= `30625/88`
= 348.011 cm3
Surface area = 2πrh
= `2 xx 22/7 xx 175/44 xx 7`
= `44/44 xx 175`
= 175 cm2
APPEARS IN
संबंधित प्रश्न
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm in following figure. The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2. Find the total expenses required for polishing and painting the surface of the bookshelf.

Find the volume of a cuboid whose length = 15 cm, breadth = 2.5 dm, height = 8 cm.
Find the height of a cuboid of volume 100 cm3, whose length and breadth are 5 cm and 4 cm respectively.
A cuboidal vessel is 10 cm long and 5 cm wide. How high it must be made to hold 300 cm3 of a liquid?
A village, having a population of 4000, requires 150 litres water per head per day. It has a tank which is 20 m long, 15 m broad and 6 m high. For how many days will the water of this tank last?
A closed rectangular box is made of wood of 1.5 cm thickness. The exterior length and breadth are respectively 78 cm and 19 cm, and the capacity of the box is 15 cubic decimeters. Calculate the exterior height of the box.
75 persons can sleep in a room 25 m by 9.6 m. If each person requires 16 m3 of the air; find the height of the room.
Four cubes, each of edge 9 cm, are joined as shown below :

Write the dimensions of the resulting cuboid obtained. Also, find the total surface area and the volume
The internal length, breadth, and height of a closed box are 1 m, 80 cm, and 25 cm. respectively. If its sides are made of 2.5 cm thick wood; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
