Advertisements
Advertisements
Question
Find the volume and total surface area of a cube whose each edge is:
(i) 8 cm
(ii) 2 m 40 cm.
Solution 1
(i)
Edge of the given cube = 8 cm
Volume of the given cube = (Edge)3 = (8)3 = 8 x 8 x 8 = 512 cm3
Total surface area of a cube = 6(Edge)2 = 6 x (8)2 = 384 cm2
(ii)
Edge of the given cube = 2 m 40 cm = 2.40 m
Volume of a cube = (Edge)3
Volume of the given cube = (2.40)3 = 2.40 x 2.40 x 2.40 = 13.824 m2
Total surface area of the given cube = 6 x 2.4 x 2.4 = 34.56 m2
Solution 2
Formulae for a Cube:
Volume (V): V = a3
Total Surface Area (TSA): TSA = 6a2
(i) Edge length = 8 cm
Volume: V = a3 = 83 = 512 cm3
Total Surface Area: TSA = 6a2 = 6 × 82 = 6 × 64 = 384 cm2
(ii) Edge length = 2 m 40 cm
Convert 2 m 40 cm to centimeters:
2 m = 200 cm, so, 2 m 40 cm = 200 + 40 = 240 cm.
Volume: V = a3 = 2403 = 240 × 240 × 240 = 13,824,000 cm3
Convert to cubic meters:
1 m3 = 1,000,000 cm3 `=>V = (1,38,24,000)/(10,00,000) = 13.224 m^3`
Total Surface Area:
TSA = 6a2 = 6 × 2402 = 6 × 57,600 = 345,600 cm2
Convert to square meters:
`1 m^2 = 10000 cm^2 => TSA = 345600/10000 = 34.56 m^2`
APPEARS IN
RELATED QUESTIONS
The floor of a rectangular hall has a perimeter 250 m. If the cost of panting the four walls at the rate of Rs.10 per m2 is Rs.15000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area.]
Find the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3?
A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
A 4 cm cube is cut into 1 cm cubes. Calculate the total surface area of all the small cubes.
Hameed has built a cubical water tank with lid for his house, with each other edge 1 .5 m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm. Find how much he would spend for the tiles, if the cost of tiles is Rs. 360 per dozen.
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs. 5 per metre sheet, sheet being 2 m wide.
Ravish wanted to make a temporary shelter for his car by making a box-like structure with tarpaulin that covers all the four sides and the top of the car ( with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m with
base dimensions 4 m × 3m?
What will happen to the volume of a cuboid if its Length is doubled, height is doubled and breadth is sama?
How many wooden cubical blocks of side 25 cm can be cut from a log of wood of size 3 m by 75 cm by 50 cm, assuming that there is no wastage?
The volume of a cuboidal box is 48 cm3. If its height and length are 3 cm and 4 cm respectively, find its breadth.
The perimeter of a floor of a room is 30 m and its height is 3 m. Find the area of four walls of the room.
If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that \[\frac{1}{V} = \frac{2}{S}\left( \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \right)\]
A tank open at the top is made of iron sheet 4 m wide. If the dimensions of the tank are 12 m × 8 m × 6 m, find the cost of iron sheet at Rs 17.50 per metre.
The cost of preparing the walls of a room 12 m long at the rate of Rs 1.35 per square metre is Rs 340.20 and the cost of matting the floor at 85 paise per square metre is Rs 91.80. Find the height of the room.
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the wall.
If two cubes each of side 6 cm are joined face to face, then find the volume of the resulting cuboid.
Volume of a cuboid is 12 cm3. The volume (in cm3) of a cuboid whose sides are double of the above cuboid is
The number of cubes of side 3 cm that can be cut from a cuboid of dimensions 10 cm × 9 cm × 6 cm, is ______.
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is ` 5 sqrt(5)` cm. Its surface area is
Total surface area of a box of cuboid shape is 500 sq. unit. Its breadth and height is 6 unit and 5 unit respectively. What is the length of that box ?
The capacity of a rectangular tank is 5.2 m3 and the area of its base is 2.6 x 104 cm2; find its height (depth).
The external dimensions of an open wooden box are 65 cm, 34 cm, and 25 cm. If the box is made up of wood 2 cm thick, find the capacity of the box and the volume of wood used to make it.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
A matchbox is 4 cm long, 2.5 cm broad, and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?
The length, breadth, and height of a rectangular solid are in the ratio 6 : 4 :3. If the total surface area is 1728 cm2. Find its dimensions.
The surface area of a cuboid formed by joining two cubes of side a face to face is ______.
Two cuboids with equal volumes will always have equal surface areas.
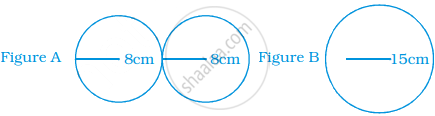
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?
A rectangular sheet of dimensions 25 cm × 7 cm is rotated about its longer side. Find the volume and the whole surface area of the solid thus generated.
