Advertisements
Advertisements
Question
Find the equation of a circle of radius 5 which is touching another circle x2 + y2 – 2x – 4y – 20 = 0 at (5, 5).
Sum
Solution
Given circle is x2 + y2 – 2x – 4y – 20 = 0
2g = – 2
⇒ g = – 1
2f = – 4
⇒ f = – 2
∴ Centre C1 = (1, 2)
And r = `sqrt(g^2 + f^2 - c)`
= `sqrt(1 + 4 + 20)`
= 5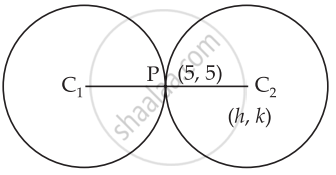
Let the centre of the required circle be (h, k).
Clearly, P is the mid-point of C1C2
∴ 5 = `(1 + h)/2`
⇒ h = 9
And 5 = `(2 + k)/2`
⇒ k = 8
Radius of the required circle = 5
∴ Equation of the circle is (x – 9)2 + (y – 8)2 = (5)2
⇒ x2 + 81 – 18x + y2 + 64 – 16y = 25
⇒ x2 + y2 – 18x – 16y + 145 – 25 = 0
⇒ x2 + y2 – 18x – 16y + 120 = 0
Hence, the required equation is x2 + y2 – 18x – 16y + 120 = 0.
shaalaa.com
Is there an error in this question or solution?
