Question

Find the equation of a circle of radius 5 which is touching another circle x² + y² – 2x – 4y – 20 = 0 at (5, 5).

Answer 1

Given circle is x² + y² – 2x – 4y – 20 = 0

2g = – 2

⇒ g = – 1

2f = – 4

⇒ f = – 2

∴ Centre C₁ = (1, 2)

And r = `sqrt(g^2 + f^2 - c)`

= `sqrt(1 + 4 + 20)`

= 5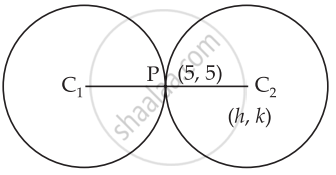

Let the centre of the required circle be (h, k).

Clearly, P is the mid-point of C₁C₂

∴ 5 = `(1 + h)/2`

⇒ h = 9

And 5 = `(2 + k)/2`

⇒ k = 8

Radius of the required circle = 5

∴ Equation of the circle is (x – 9)² + (y – 8)² = (5)²

⇒ x² + 81 – 18x + y² + 64 – 16y = 25

⇒ x² + y² – 18x – 16y + 145 – 25 = 0

⇒ x² + y² – 18x – 16y + 120 = 0

Hence, the required equation is x² + y² – 18x – 16y + 120 = 0.