Question

Find the equation of a circle whose centre is (3, –1) and which cuts off a chord of length 6 units on the line 2x – 5y + 18 = 0.

Answer 1

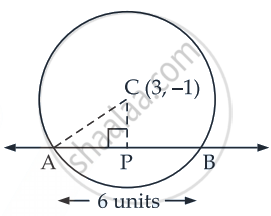
Given that: Centre of the circle = (3, – 1)

Length of chord AB = 6 units

CP = `|(2 xx 3 - 5 xx - 1 + 18)/sqrt((2)^2 + (-5)^2)|`

= `|(6 + 5 + 18)/sqrt(29)|`

= `sqrt(29)`

Now AB = 6 units.

∴ AP = `1/2 "AB" = 1/2 xx 6` = 3 units

In ΔCPA, AC² = CP² + AP²

= `(sqrt(29))^2 + (3)^2`

= 29 + 9

= 38

∴ AC = `sqrt(38)`

So, the radius of the circle, r = `sqrt(38)`

∴ Equation of the circle is (x – 3)² + (y + 1)² = `(sqrt(38))^2`

⇒ (x – 3)² + (y + 1)² = 38

⇒ x² + 9 – 6x + y² + 1 + 2y = 38

⇒ x² + y² – 6x + 2y = 28

Hence, the required equation is x² + y² – 6x + 2y = 28.