Question

Find the equation of the median and altitude of ΔABC through A where the vertices are A(6, 2), B(– 5, – 1) and C(1, 9)

Answer 1

(i) To find the median

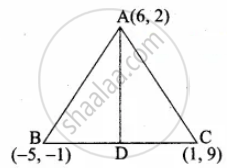
Mid point of BC (D) = `((x_1 +x_2)/2, (y_1 + y_2)/2)`

= `((-5 + 1)/2, (-1 + 9)/2)`

= `((-4)/2, 8/2)`

= (– 2, 4)

Equation of the median AD is

`(y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1)`

`(y - 2)/(4 - 2) = (x - 6)/(-2 - 6)`

`(y - 2)/2 = (x - 6)/(-8)`

2(x – 6) = – 8(y – 2)

2x – 12 = – 8y + 16

2x + 8y – 28 = 0

x + 4y – 14 = 0  ...(÷ by 2) 

∴ Equation of the median is x + 4y – 14 = 0

Equation of the altitude is 3x + 5y – 28 = 0

(ii) To find the equation of the altitude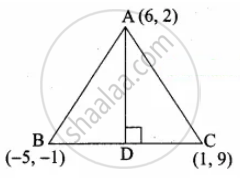

Slope of BC = `(y_2 - y_1)/(x_2 - x_1)`

= `(9 + 1)/(1 + 5)`

= `10/6`

= `5/3`

Slope of the altitude = `-3/5`

Equation of the altitude AD is

y – y₁ = m (x – x₁)

y – 2 = `– 3/5` (x – 6)

– 3(x – 6) = 5(y – 2)

– 3x + 18 = 5y – 10

– 3x – 5y + 18 + 10 = 0

– 3x – 5y + 28 = 0

3x + 5y – 28 = 0