Advertisements
Advertisements
Question
Find the values of m and n if the following polynomial is a perfect square
`1/(x^4) - 6/(x^3) + 13/(x^2) + "m"/x + "n"`
Solution
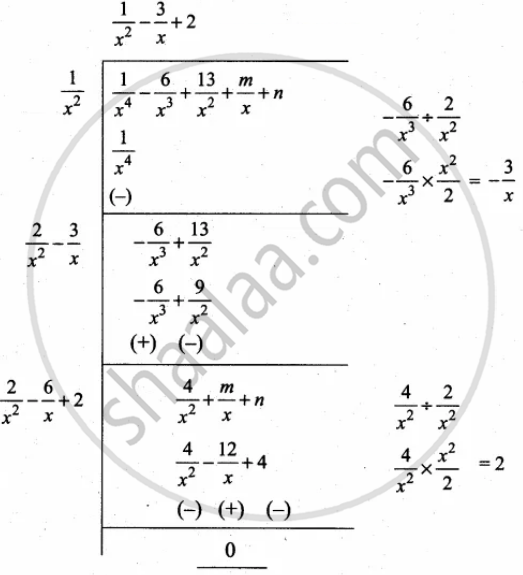
Since it is a perfect square
`1/x` (m + 12) = 0
m + 12 = 0
m = – 12
n – 4 = 0
n = 4
∴ The value of m = – 12 and n = 4
APPEARS IN
RELATED QUESTIONS
Find the square root of the following rational expression
`(7x^2 + 2sqrt(14)x + 2)/(x^2 - 1/2 x + 1/16)`
Find the square root of the following rational expression
`(121("a" + "b")^8 (x + y)^8 ("b" - "c")^8)/(81("b" - "c")^4 ("a" - "b")^12 ("b" - "c")^4)`
Find the square root of the following
`1 + 1/(x^6) + 2/(x^3)`
Find the square root of the following
(4x2 – 9x + 2)(7x2 – 13x – 2)(28x2 – 3x – 1)
Find the square root of the following polynomials by division method
37x2 – 28x3 + 4x4 + 42x + 9
The square root of `(256x^8y^4z^10)/(25x^6y^6z^6)` is equal to
Which of the following should be added to make x4 + 64 a perfect square
Find the square root of 289x4 – 612x3 + 970x2 – 684x + 361
If α and β are the roots of the polynomial f(x) = x2 – 2x + 3, find the polynomial whose roots are α + 2, β + 2
If α and β are the roots of the polynomial f(x) = x2 – 2x + 3, find the polynomial whose roots are `(alpha - 1)/(alpha + 1), (beta - 1)/(beta + 1)`
