Advertisements
Advertisements
Question
Find the volume of a cylinder, the diameter of whose base is 7 cm and height being 60 cm. Also, find the capacity of the cylinder in litres.
Solution
Given:
Diameter, d = 7 cm
Radius, r = 3 . 5 cm
Height, h = 60 cm
\[\text{ Volume of the cylinder, V }= \pi r^2 h\]
\[ = \frac{22}{7} \times 3 . 5^2 \times 60\]
\[ = 2310 {cm}^3 \]
\[\text{ Capacity of the cylinder in litres }= \frac{2310}{1000} \left( 1\text{ litre }= 1000\text{ cubic cm }\right)\]
\[ = 2 . 31 L\]
APPEARS IN
RELATED QUESTIONS
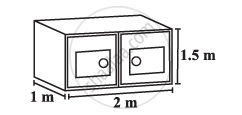
Rukhsar painted the outside of the cabinet, of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?
A solid cylinder has total surface area of 462 cm2. Its curved surface area is one-third of its total surface area. Find the radius and height of the cylinder.
The students of a Vidyalaya were asked to participate in a competition for making and decorating pen holders in the shape of a cylinder with a base, using cardboard. Each pen holder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions moving once over to level a playground. What is the area of the playground?
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. Calculate the ratio of their volumes.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
If the height of a cylinder is doubled and radius remains the same, then volume will be ______.
Find the total surface area of a closed cylindrical drum if its diameter is 50 cm and height is 45 cm. (π = 3.14)
Find
How much steel was actually used, if `1/12` of the steel actually used was wasted in making the tank.
`["Assume "pi=22/7]`
The ratio of the radius and height of a cylinder is 2:3. If its volume is 12,936 cm3, find the total surface area of the cylinder.
