Advertisements
Advertisements
Question
Find the volume of the solid generated, when the area between ellipse 4x2 + 9y2 = 36 and the chord AB, with A (3, 0), B (0, 2), is revolved about X-axis.
Solution
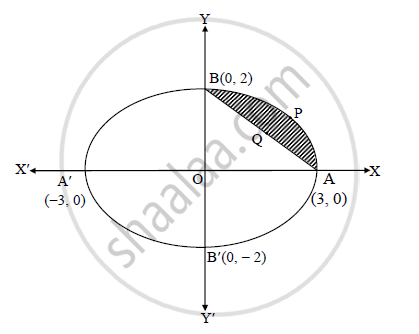
Given equation of ellipse is 4x2 + 9y2 = 36
`:. y^2 = 4/9(9 - x^2)`.....(i)
and equation of the chord is `x/3 + y/2 = 1`
∴ 2x + 3y = 6
∴ 3y = 6 − 2x
∴ y = 2 − `2/3x`
∴ `y^2 = (2 - 2/3 x)^2 = 4 - 8/3x + 4/9 x^2 ` ....(ii)
Required solid is obtained by revolving the shaded region about the X-axis between x = 0 and x = 3.
Let V1 = volume of solid obtained by revolving the region OAPBO under the ellipse
V2
= volume of solid obtained by revolving the region OAQBO under the chord AB.
∴ V = V1 − V2
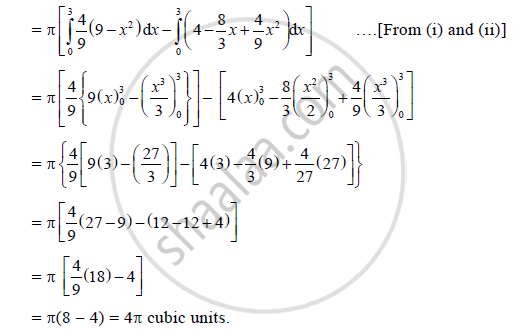
shaalaa.com
Is there an error in this question or solution?
