Advertisements
Advertisements
Question
For each of the following statements state whether true(T) or false (F)
the ratio of the perimeter of two similar triangles is the same as the ratio of the their corresponding medians.
Solution
True
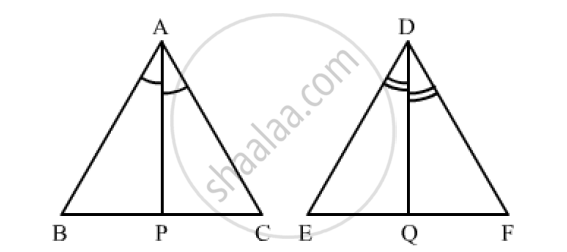
Given: ΔABC ~ ΔDEF
To prove=`(Ar(ΔABC))/(Ar(ΔDEF))=((AP)/(DQ))^2`
Proof: in ΔABP and ΔDEQ
∠๐ต๐ด๐= ∠๐ธ๐ท๐ (๐ด๐ ∠๐ด= ∠๐ท,๐ ๐ ๐กโ๐๐๐ ๐ป๐๐๐ ๐๐ ๐๐๐ ๐ ๐๐๐ข๐๐)
∠๐ต= ∠๐ธ (∠๐ด๐ต๐ถ ~ Δ๐ท๐ธ๐น)
By AA criterion, ΔABP and ΔDEQ
`(AB)/(DE)=(AP)/(DQ)` .................(1)
Since, ΔABC ~ ΔDEF
∴ `(Ar(ΔABC))/(Ar(ΔDEF))=((AB)/(DE))^2`
⇒ `(Ar(ΔABC))/(Ar(ΔDEF))=((AP)/(DQ))^2` [๐๐ ๐๐๐ (1)]
APPEARS IN
RELATED QUESTIONS
Give two different example of a pair of similar figures.
State whether the following quadrilaterals are similar or not:
Write the truth value (T/F) of each of the following statement
Two polygons are similar, if their corresponding sides are proportional.
For each of the following statements state whether true(T) or false (F)
Two circles with different radii are similar.
For each of the following statements state whether true(T) or false (F)
any two rectangles are similar
For each of the following statements state whether true(T) or false (F)
the polygon formed by joining the midpoints of the sides of a quadrilateral is a rhombus.
If O is Any Point Inside a Rectangle Abcd Then `Oa^2+Oc^2=Ob^2+Od^2`
If in two As ABC and DEF, `"AB"/"DF" = "BC"/"FE" = "CA"/"ED"`, then ______.
The lengths of the diagonals of a rhombus are 24cm and 32cm, then the length of the altitude of the rhombus is ______.
Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1cm. Total area of all the dotted regions assuming the thickness of the rings to be negligible is ______.
