Advertisements
Advertisements
Question
For light diverging from a point source ______.
- the wavefront is spherical.
- the intensity decreases in proportion to the distance squared.
- the wavefront is parabolic.
- the intensity at the wavefront does not depend on the distance.
Options
a and b
a and c
b and c
c and d
Solution
a and b
Explanation:
| Type of wavefront | Intensity | Amplitude |
Spherical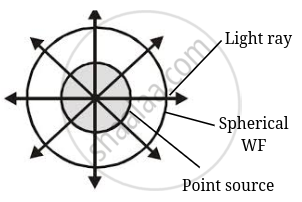 |
`I oo 1/r^2` | `A oo 1/r` |
Cylindrical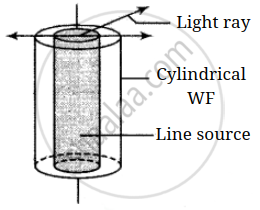 |
`I oo 1/r` | `A oo 1/sqrt(r)` |
Plane |
`I oo 1/r^0` | `A oo r^0` |
Due to the point source light propagates in all directions symmetrically and hence, wavefront will be spherical as shown in the diagram.
As intensity of the source will be `I oo 1/r^2`
Where r is radius of the wavefront at any time.
Hence the intensity decreases in proportion to the distance squared.
APPEARS IN
RELATED QUESTIONS
State Huygen's principle.
Use Huygens' principle to verify the laws of refraction.
Using this principle draw a diagram to show how a plane wave front incident at the interface of the two media gets refracted when it propagates from a rarer to a denser medium. Hence verify Snell's law of refraction.
State Huygens’s principle. Show, with the help of a suitable diagram, how this principle is used to obtain the diffraction pattern by a single slit.
Draw a plot of intensity distribution and explain clearly why the secondary maxima becomes weaker with increasing order (n) of the secondary maxima.
Light waves travel in vacuum along the X-axis. Which of the following may represent the wave fronts?
Wavefront means
Figure shows a standard two slit arrangement with slits S1, S2, P1, P2 are the two minima points on either side of P (Figure). At P2 on the screen, there is a hole and behind P2 is a second 2-slit arrangement with slits S3, S4 and a second screen behind them.
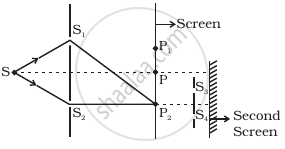
Is Huygen’s principle valid for longitudinal sound waves?
Two light beams of intensities in the ratio of 9 : 4 are allowed to interfere. The ratio of the intensity of maxima and minima ______.
According to Huygens's principle, the amplitude of secondary wavelets is ______.
