Advertisements
Advertisements
Question
For two vectors A and B, A + B = A − B is always true when
- |A| = |B| ≠ 0
- A ⊥ B
- |A| = |B| ≠ 0 and A and B are parallel or anti parallel
- When either |A| or |B| is zero
Solution
b and d
Explanation:
Given, `|A + B| = |A - B|`
⇒ `sqrt(|A|^2 + |B|^2 + 2|A||B| cos theta) = sqrt(|A|^2 + |B|^2 - 2|A||B| cos theta)`
⇒ `|A|^2 + |B|^2 + 2|A||B| cos theta = |A|^2 + |B|^2 - 2|A||B| cos theta`
⇒ `4 |A||B| cos theta` = 0
⇒ `|A||B| cos theta` = 0
⇒ `|A|` = 0 or `|B|` = 0 or cos θ = 0
⇒ θ = 90°
When θ = 90°, we can say that A ⊥ B.
APPEARS IN
RELATED QUESTIONS
Given a + b + c + d = 0, state whether the following statement is correct or incorrect:
b + c must lie in the plane of a and d if a and d are not collinear, and in the line of a and d, if they are collinear.
Establish the following vector inequalities geometrically or otherwise:
- | a+b | ≤ |a| + |b|
- |a + b| ≥ | |a| - |b| |
- |a - b| ≤ |a| + |b|
- |a-b| ≥ | |a| - |b| |
When does the equality sign above apply?
Given a + b + c + d = 0, state whether the following statement is correct or incorrect:
The magnitude of (a + c) equals the magnitude of (b + d).
Given a + b + c + d = 0, state whether the following statement is correct or incorrect:
The magnitude of a can never be greater than the sum of the magnitudes of b, c, and d.
The resultant of two vectors `vecA` and `vecB` is `vecC`. If the magnitude of `vecB` is doubled, the new resultant vector becomes perpendicular to `vecA`, then the magnitude of `vecC` is
Given below in column I are the relations between vectors a, b and c and in column II are the orientations of a, b and c in the XY plane. Match the relation in column I to correct orientations in column II.
| Column I | Column II | ||
| (a) | a + b = c | (i) | 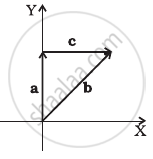 |
| (b) | a – c = b | (ii) |  |
| (c) | b – a = c | (iii) | 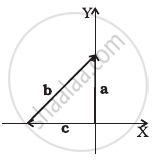 |
| (d) | a + b + c = 0 | (iv) | 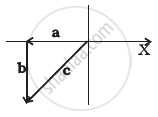 |
If `vecA` and `vecB` is two vectors satisfying the relation `vecA.vecB = [vecA xx vecB]`. Then the value of `[vecA - vecB]` will be ______.
If `vec"A" = (2hat"i"+3hat"j"- hat"k")`m and `vec"B" = (hat"i" + 2hat"j"+ 2hat"k")` m. The magnitude of component of vector `vec"A"` along vector `vec"B"` will be ______ m.
