Advertisements
Advertisements
Question
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read at least one of the newspapers
Solution
Let M = set of individuals who read Marathi newspapers
E = set of individuals who read English newspapers
X = set of all literate individuals
∴ n(X) = 2000, n(M)
= `70/100xx2000`
= 1400
n(E) = `50/100xx2000` = 1000
n(M ∩ E) = `32.5/100xx2000` = 650
n(M ∪ E) = n(M) + n(E) − n(M ∩ E)
= 1400 + 1000 − 650
= 1750
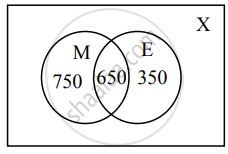
No. of individuals who read at least one of the newspapers = n(M ∪ E) = 1750.
APPEARS IN
RELATED QUESTIONS
Identify whether the following is set or not? Justify your answer.
The collection of questions in this Chapter.
Write the following set in roster form:
E = The set of all letters in the word TRIGONOMETRY
Write the following set in the set-builder form:
{3, 6, 9, 12}
Write the following set in the set-builder form:
{2, 4, 6, …}
Write the following set in the set-builder form:
{1, 4, 9, ....., 100}
List all the elements of the following set:
D = {x : x is a letter in the word “LOYAL”}
List all the elements of the following set:
E = {x : x is a month of a year not having 31 days}
Which of the following collection is set? Justify your answer:
The collection of ten most talented writers of India.
Describe the following sets in Roster form:
{x : x is a letter before e in the English alphabet}
Describe the following sets in Roster form:
{x ∈ N : x is a prime number, 10 < x < 20};
Describe the following sets in set-builder form:
A = {1, 2, 3, 4, 5, 6}
Which of the following statements are correct?
Write a correct form of each of the incorrect statement.
\[a \in {\left\{ a \right\}, b}\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\phi \in A\]
Write down all possible subsets of each of the following set:
{0, 1},
Write down all possible subsets of each of the following set:
{1, {1}},
If A is any set, prove that: \[A \subseteq \phi \Leftrightarrow A = \phi .\]
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, = {2, 4, 6, 8} and C = {3, 4, 5, 6}.
Find \[\left( A \cap C \right)'\]
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
10 _____ A
Describe the following set in Set-Builder form
`{1/2, 2/5, 3/10, 4/17, 5/26, 6/37, 7/50}`
If A = {x/6x2 + x – 15 = 0}, B = {x/2x2 – 5x – 3 = 0}, C = {x/2x2 – x – 3 = 0} then find (A ∩ B ∩ C)
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read Only one of the newspapers
Write the following interval in Set-Builder form:
[6, 12]
Write the following sets in the roaster form.
A = {x | x is a positive integer less than 10 and 2x – 1 is an odd number}
Write the following sets in the roaster from:
C = {x | x is a positive factor of a prime number p}
Write the following sets in the roaster form:
F = {x | x4 – 5x2 + 6 = 0, x ∈ R}
If Y = {x | x is a positive factor of the number 2p – 1 (2p – 1), where 2p – 1 is a prime number}.Write Y in the roaster form.
State which of the following statement is true and which is false. Justify your answer.
35 ∈ {x | x has exactly four positive factors}.
State which of the following statement is true and which is false. Justify your answer.
3 ∉ {x | x4 – 5x3 + 2x2 – 112x + 6 = 0}
Determine whether the following statement is true or false. Justify your answer.
For all sets A, B, and C, A – (B – C) = (A – B) – C
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in more than one subject only
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is ______.
A survey shows that 63% of the people watch a News Channel whereas 76% watch another channel. If x% of the people watch both channel, then ______.
State True or False for the following statement.
Given A = {0, 1, 2}, B = {x ∈ R | 0 ≤ x ≤ 2}. Then A = B.
