Question

From a lot of 6 items containing 2 defective items, a sample of 4 items are drawn at random. Let the random variable X denote the number of defective items in the sample.

If the sample is drawn without replacement, find :

1) The probability distribution of X

2) Mean of X

3) Variance of X

Answer 1

In 6 items 2 defectives and 4 non-defective

Let P is the probability of defective items

Let x = number of defective items

`:. x = 0,1,2`

`:. P(x= 0) = (""^4C_4)/(""^6C_4) = 1/15`

`:. P(x = 1) = (""^2C_1xx""^4C_3)/(""^6C_4) = 8/15`

`:. P(x = 2) = (""^2C_2 xx""^4C_2)/(""^6C_4) = 6/15`

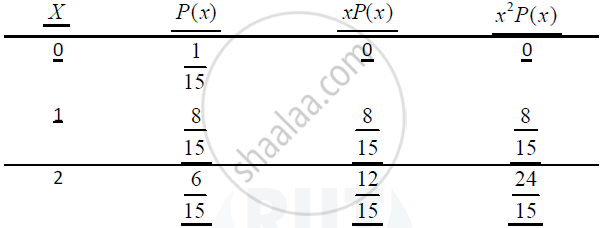
b) `Mean(barX) = sumP_iX_i`

= `20/15 = 4/3`

c) A variance of `(sigma^2) = sumP_iX_i^2 - (EP_iX_i)^2`

`= 32/15 - (4/3)^2 = 16/45 = 0.35`