Question

ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:

निम्न अवरोधों के अंतर्गत Z = -3x + 4y का न्यूनतमीकरण कीजिए:

x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0

Answer 1

बाधाओं की प्रणाली है,

x + 2y ≤ 8                   ....(i)

3x + 2y ≤ 12                ....(ii)

और x ≥ 0, y ≥ 0         ...(iii)

माना `l_1: x + 2y = 8;  l_2: 3x + 2y = 12`

चित्र में छायांकित क्षेत्र बाधाओं (i) से (iii) की प्रणाली द्वारा निर्धारित व्यवहार्य क्षेत्र है।

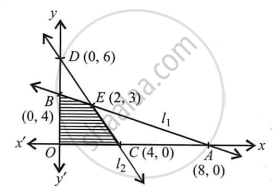
यह देखा गया है कि सुसंगत क्षेत्र OCEB परिबद्ध है।

इस प्रकार

इस प्रकार, हम Z का न्यूनतम मान निर्धारित करने के लिए कोना बिंदु विधि का उपयोग करते हैं।

हमारे पास है, Z = - 3x + 4y

O, C, E और B के निर्देशांक (0, 0), (4, 0), (2, 3) हैं।

(x + 2y = 8 और 3x + 2y = 12 को हल करने पर) और क्रमशः (0, 4)

अंक	Z के संगत मान
(0, 0)	0
(4, 0)	-12 (न्यूनतम)
(2, 3)	6
(0, 4)	16

सपश्त है की Z की न्यूनतम मात्रा -12 है जो अंक A(4, 0) पर है |