Advertisements
Advertisements
Question
Give an account of magnetic Lorentz force.
Numerical
Solution
(a)

(b)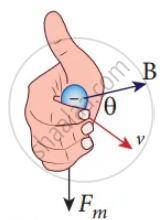
Direction of the Lorentz force on
(a) positive charge
(b) negative charge
- An electric charge q is moving with velocity `vec"v"` in the magnetic field `vec"B"`, experience a force called magnetic force `vec"F"_"m"` deduced by Lorentz.
`vec"F"_"m" = "q" (vec"v" xx vec"B")` ....(1)
`vec"F"_"m"` = qvBsin θ ……………(2)Equations (1) & (2) implies
- `vec"F"_"m"` is directly proportional to the magnetic field `vec"B"`.
- `vec"F"_"m"` is directly proportional to the velocity `vec"V"`.
- `vec"F"_"m"` is directly proportional to sine of the angle between the velocity and magnetic field.
- `vec"F"_"m"` is directly proportional to the magnitude of the charge q.
- `vec"F"_"m"` is always perpendicular to `vec"V" and vec"B".`
- The direction `vec"F"_"m"` on negative charge is opposite to the direction of `vec"F"_"m"` on positive charge.
- If velocity `vec"v"` of the charge is along magnetic field, `vec"F"_"m" = 0.`
shaalaa.com
Lorentz Force
Is there an error in this question or solution?
Chapter 3: Magnetism and magnetic effects of electric current - Evaluation [Page 192]
APPEARS IN
RELATED QUESTIONS
What is resonance condition in cyclotron?
State Fleming’s left-Hand rule.
Is an ammeter connected in series or parallel in a circuit? Why?
Explain the concept of velocity selector.
Discuss the working of cyclotron in detail.
Derive the expression for the force between two parallel, current-carrying conductors.
