Advertisements
Advertisements
Question
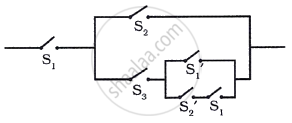
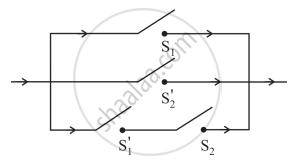
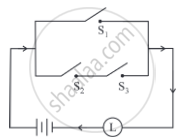
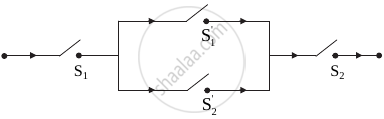
Give an alternative equivalent simple circuit for the following circuit:
Solution
Let p: the switch S1 is closed
q: the switch S2 is closed
r: the switch S3 is closed
∼ q: the switch S2′ is closed or the switch S2 is open
∼ r: the switch S3′ is closed or the switch S3 is open.
Then the symbolic form of the given circuit is:
[p ∧ (q ∨ r)] ∨ (∼ r ∧ ∼ q ∧ p)
Using the laws of logic, we have
[p ∧ (q ∨ r)] ∨ (∼ r ∧ ∼ q ∧ p)
≡ [p ∧ (q ∨ r)] ∨ [∼ (r ∨ q) ∧ p] .......(By De Morgan’s Law)
≡ [p ∧ (q ∨ r)] ∨ [p ∧ ∼ (q ∨ r)] ......(By Commutative Law)
≡ p ∧ [(q ∨ r) ∨ ∼ (q ∨ r)] ...........(By Distributive Law)
≡ p ∧ T ...........(By Complement Law)
≡ p .........(By Identity Law)
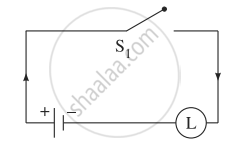
Hence, the alternative equivalent simple circuit is
APPEARS IN
RELATED QUESTIONS
Construct the switching circuit for the following statement : [p v (~ p ∧ q)] v [(- q ∧ r) v ~ p]
Construct the simplified circuit for the following circuit:
Find the symbolic form of the following switching circuit, construct its switching table and interpret it.
Construct the switching circuit for the statement (p ∧ q) ∨ (~ p) ∨ (p ∧ ~ q).
Simplify the following circuit so that the new circuit has minimum number of switches. Also, draw the simplified circuit.
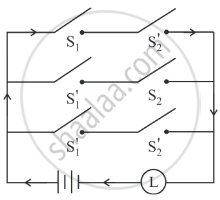
Construct the new switching circuit for the following circuit with only one switch by simplifying the given circuit:
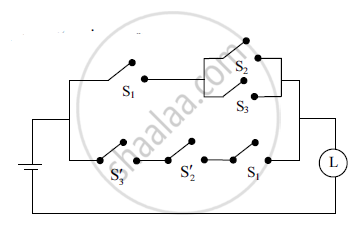
Find the symbolic form of the given switching circuit. Construct its switching table and interpret your result.
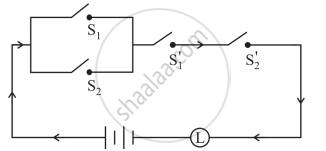
Express the following circuit in the symbolic form of logic and writ the input-output table.
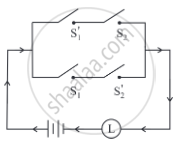
Express the following circuit in the symbolic form of logic and write the input-output table.
Express the following circuit in the symbolic form of logic and write the input-output table.

Express the following circuit in the symbolic form of logic and writ the input-output table.

Express the following circuit in the symbolic form of logic and writ the input-output table.
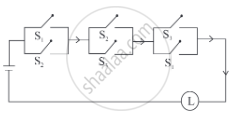
Construct the switching circuit of the following:
(∼ p ∧ q) ∨ (p ∧ ∼ r)
Construct the switching circuit of the following:
(p ∧ q) ∨ [∼ p ∧ (∼ q ∨ p ∨ r)]
Construct the switching circuit of the following:
(p ∧ r) ∨ (∼ q ∧ ∼ r)] ∧ (∼ p ∧ ∼ r)
Construct the switching circuit of the following:
(p ∧ ∼ q ∧ r) ∨ [p ∧ (∼ q ∨ ∼ r)]
Construct the switching circuit of the following:
p ∨ (∼ p) ∨ (∼ q) ∨ (p ∧ q)
Construct the switching circuit of the following:
(p ∧ q) ∨ (∼ p) ∨ (p ∧ ∼ q)
Give an alternative equivalent simple circuit for the following circuit:

Write the symbolic form of the following switching circuit construct its switching table and interpret it.
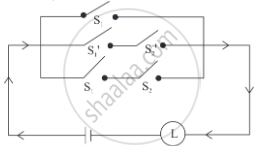
Write the symbolic form of the following switching circuit construct its switching table and interpret it.

Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
p ∨ (q ∧ ∼ q)
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(∼ p ∧ q) ∨ (∼ p ∧ ∼ q) ∨ (p ∧ ∼ q)
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
[p ∨ ( ∼ q) ∨ (∼ r)] ∧ [p ∨ (q ∧ r)]
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(p ∧ q ∧ ∼ p) ∨ (∼ p ∧ q ∧ r) ∨ (p ∧ ∼ q ∧ r) ∨ (p ∧ q ∧ r)
Express the following circuit in the symbolic form. Prepare the switching table:
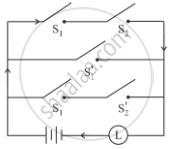
Express the following circuit in the symbolic form. Prepare the switching table:
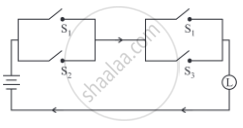
Simplify the following so that the new circuit has a minimum number of switches. Also, draw the simplified circuit.
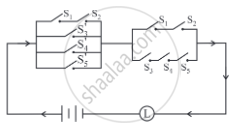
Check whether the following switching circuits are logically equivalent - Justify.
(i)
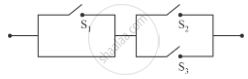
(ii)

Check whether the following switching circuits are logically equivalent - Justify.
(i)
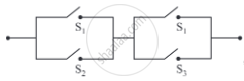
(ii)
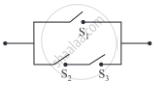
Give alternative arrangement of the switching following circuit, has minimum switches.
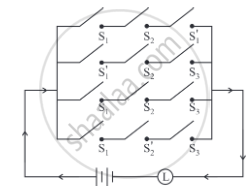
Simplify the following so that the new circuit.
A stone is dropped into a pond. Waves in the form of circles are generated and radius of outermost ripple increases at the rate of 5 cm/sec. Then area increased after 2 seconds is ______.
Simplify the given circuit by writing its logical expression. Also, write your conclusion.
Construct the switching circuit for the following logical statement:
(p ∨ ∼ q) ∨ (q ∧ r). Also construct the switching circuit for its simplified form.
Find the alternative arrangement using minimum switches for the following switching circuit.