Advertisements
Advertisements
Question
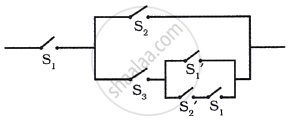
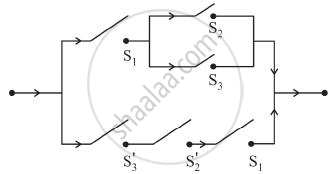
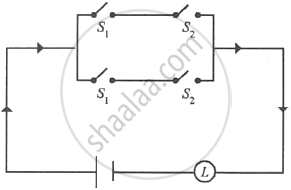
Simplify the following so that the new circuit has a minimum number of switches. Also, draw the simplified circuit.
Solution
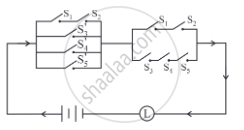
Let p: the switch S1 is closed
q: the switch S2 is closed
r: the switch S3 is closed
s: the switch S4 is closed
t: the switch S5 is closed
∼p: the switch S1′ is closed or the switch S1 is open
∼q: the switch S2′ is closed or the switch S2 is open
∼r: the switch S3′ is closed or the switch S3 is open
∼s: the switch S4′ is closed or the switch S4 is open
∼t: the switch S5′ is closed or the switch S5 is open.
Then the given circuit in symbolic form is:
[(p ∧ q) ∨ ∼r ∨ ∼s ∨ ∼t] ∧ [(p ∧ q) ∨ (r ∧ s ∧t )]
Using the laws of logic, we have,
[(p ∧ q) ∨ ∼r ∨ ∼s ∨ ∼t] ∧ [(p ∧ q) ∨ (r ∧ s ∧t )]
≡ [(p ∧ q) ∨ ∼ (r ∧ s ∧ t)] ∧ [(p ∧ q) ∨ (r ∧ s ∧ t)] .........(By De Morgan’s Law)
≡ (p ∧ q) ∨ [∼ (r ∧ s ∧ t) ∧ (r ∧ s ∧ t)] ......(By Distributive Law)
≡ (p ∧ q) ∨ F ...........(By Complement Law)
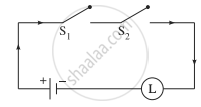
≡ p ∧ q .......(By Identity Law)
Hence, the alternative simplified circuit is:
APPEARS IN
RELATED QUESTIONS
Construct the switching circuit for the following statement : [p v (~ p ∧ q)] v [(- q ∧ r) v ~ p]
Construct the simplified circuit for the following circuit:
Find the symbolic form of the following switching circuit, construct its switching table and interpret it.
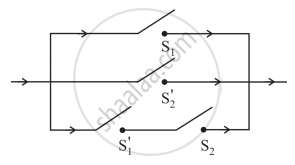
Construct the switching circuit for the statement (p ∧ q) ∨ (~ p) ∨ (p ∧ ~ q).
Simplify the following circuit so that the new circuit has minimum number of switches. Also, draw the simplified circuit.
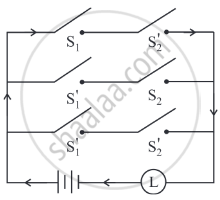
Construct the new switching circuit for the following circuit with only one switch by simplifying the given circuit:
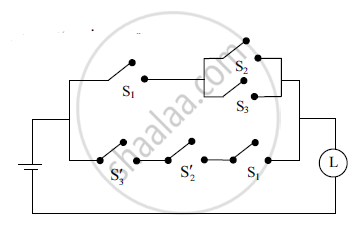
Find the symbolic form of the given switching circuit. Construct its switching table and interpret your result.
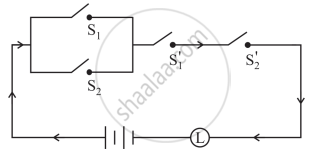
Express the following circuit in the symbolic form of logic and writ the input-output table.
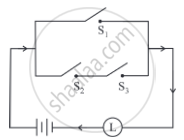
Express the following circuit in the symbolic form of logic and write the input-output table.
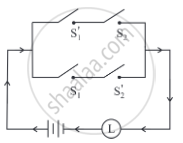
Express the following circuit in the symbolic form of logic and write the input-output table.

Express the following circuit in the symbolic form of logic and write the input-output table.
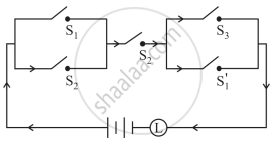
Express the following circuit in the symbolic form of logic and writ the input-output table.

Express the following circuit in the symbolic form of logic and writ the input-output table.
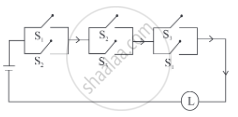
Construct the switching circuit of the following:
(p ∧ q) ∨ [∼ p ∧ (∼ q ∨ p ∨ r)]
Construct the switching circuit of the following:
(p ∧ r) ∨ (∼ q ∧ ∼ r)] ∧ (∼ p ∧ ∼ r)
Construct the switching circuit of the following:
(p ∧ ∼ q ∧ r) ∨ [p ∧ (∼ q ∨ ∼ r)]
Construct the switching circuit of the following:
p ∨ (∼ p) ∨ (∼ q) ∨ (p ∧ q)
Construct the switching circuit of the following:
(p ∧ q) ∨ (∼ p) ∨ (p ∧ ∼ q)
Give an alternative equivalent simple circuit for the following circuit:

Give an alternative equivalent simple circuit for the following circuit:
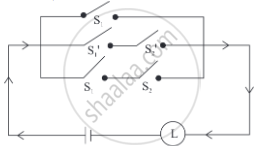
Write the symbolic form of the following switching circuit construct its switching table and interpret it.
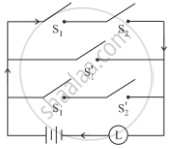
Write the symbolic form of the following switching circuit construct its switching table and interpret it.

Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
p ∨ (q ∧ ∼ q)
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(∼ p ∧ q) ∨ (∼ p ∧ ∼ q) ∨ (p ∧ ∼ q)
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
[p ∨ ( ∼ q) ∨ (∼ r)] ∧ [p ∨ (q ∧ r)]
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(p ∧ q ∧ ∼ p) ∨ (∼ p ∧ q ∧ r) ∨ (p ∧ ∼ q ∧ r) ∨ (p ∧ q ∧ r)
Express the following circuit in the symbolic form. Prepare the switching table:
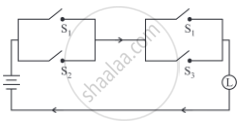
Express the following circuit in the symbolic form. Prepare the switching table:
Check whether the following switching circuits are logically equivalent - Justify.
(i)
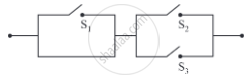
(ii)

Check whether the following switching circuits are logically equivalent - Justify.
(i)
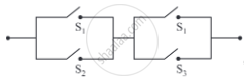
(ii)
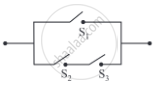
Simplify the following so that the new circuit.
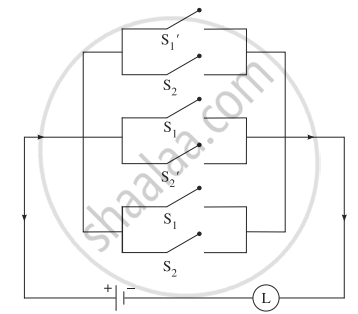
Represent the following switching circuit in symbolic form and construct its switching table. Write your conclusion from the switching table.

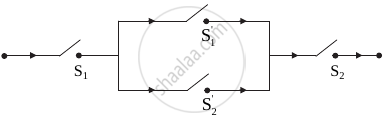
Symbolic form of the given switching circuit is equivalent to:
Simplify the given circuit by writing its logical expression. Also, write your conclusion.
Construct the switching circuit for the following logical statement:
(p ∨ ∼ q) ∨ (q ∧ r). Also construct the switching circuit for its simplified form.
Find the alternative arrangement using minimum switches for the following switching circuit.