Advertisements
Advertisements
Question
How does the time period (T) of a simple pendulum depend on its length (l)? Draw a graph showing the variation of T2 with l. How will you use this graph to determine the value of g (acceleration due to gravity)?
Advertisements
Solution
The time period of a simple pendulum is directly proportional to the square root of its effective length.
`T ∝ sqrt(l)`
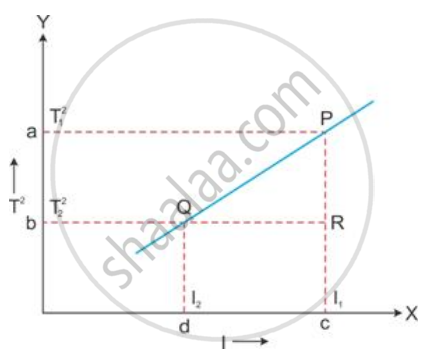
From this graph, the value of acceleration due to gravity (g) can be calculated as follows.
The slope of the straight line can be found by taking two points P and Q on the straight line and drawing normals from these points on the X- and Y-axis, respectively. Then, the value of T2 is to be noted at a and b, the value of l at c and d. Then,
Slope = `"PR"/"QR" = "ab"/"cd" = (T_1^2 - T_2^2)/(l_1 - l_2)`
This slope is found to be constant at a place and is equal to `(4pi^2)/"g"` , where g is the acceleration due to gravity at that place. Thus, g can be determined at a place from these measurements using the following relation:
`"g" = (4pi^2)/("Slope" "of" T^2 "Vs" l "graph")`
APPEARS IN
RELATED QUESTIONS
Define the terms : oscillation
What do you understand by amplitude of simple pendulum?
Two simple pendulums A and B have equal lengths, but their bobs weigh 50 gf and 100 gf, respectively. What would be the ratio of their time periods? Give reasons for your answer.
A body measures 25 m. State the unit and the magnitude of the unit in the statement.
Name the convenient unit you will use to measure:
length of a hall
Name the most convenient unit of mass you will use to measure:
Mass of small amount of medicine.
Name the most convenient unit of mass you will use to measure:
The grain output of a state
The size of bacteria is 2 μ.. Find the number of bacteria in 3 m length.
