Advertisements
Advertisements
Question
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Solution
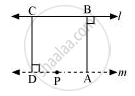
Two lines are said to be parallel if they are equidistant from one other and they do not have any point of intersection. In order to understand it easily, let us take any line l and a point P not on l. Then, by Playfair’s axiom (equivalent to the fifth postulate), there is a unique line m through P which is parallel to l.

The distance of a point from a line is the length of the perpendicular from the point to the line. Let AB be the distance of any point on m from l and CD be the distance of any point on l from m. It can be observed that AB = CD. In this way, the distance will be the same for any point on m from l and any point on l from m. Therefore, these two lines are everywhere equidistant from one another.
APPEARS IN
RELATED QUESTIONS
Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Euclidean geometry is valid only for curved surfaces.
Two distinct intersecting lines cannot be parallel to the same line.
Study the following statement:
“Two intersecting lines cannot be perpendicular to the same line”.
Check whether it is an equivalent version to the Euclid’s fifth postulate.
[Hint: Identify the two intersecting lines l and m and the line n in the above statement.]
