Advertisements
Advertisements
Question
If \[\frac{5 + 9 + 13 + . . . \text{ to n terms} }{7 + 9 + 11 + . . . \text{ to (n + 1) terms}} = \frac{17}{16},\] then n =
Options
8
7
10
11
Solution
Here, we are given,
\[\frac{5 + 9 + 13 + . . . \text{ to n terms} }{7 + 9 + 11 + . . . \text{ to (n + 1) terms}} = \frac{17}{16},\] ...........(1)
We need to find n.
So, first let us find out the sum of n terms of the A.P. given in the numerator ( 5 + 9 + 13 + ...) . Here we use the following formula for the sum of n terms of an A.P.,
`S_n = n/2 [ 2a + ( n - 1) d ]`
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
Here,
Common difference of the A.P. (d) = a2 - a1
= 9 - 5
= 4
Number of terms (n) = n
First term for the given A.P. (a) = 5
So, using the formula we get,
`S_n = n/2 [ 2(5) + ( n-1) ( 4) ] `
`= (n/2) [ 10 + (4n - 4)] `
` = ( n/2) (6 +4n) `
= n (3 + 2n) ....(2)
Similarly, we find out the sum of ( n + 1) terms of the A.P. given in the denominator ( 7 + 9 + 11+...) .
Here,
Common difference of the A.P. (d) = a2- a1
= -9 - 7
= 2
Number of terms (n) = n
First term for the given A.P. (a) = 7
So, using the formula we get,
`S_(N+1) = ( n+1)/2 [ 2(7) + [( n + 1 ) - 1](2)]`
`= ((n + 1) /2 )[14 + ( n) ( 2 ) ] `
= ( n + 1 ) ( 7 + n)
= 7n + 7 + n2 + n
= n2 + 8n + 7 ..........(3)
Now substituting the values of (2) and (3) in equation (1), we get,
`(2n^2 + 3n ) /(n^2 + 8n + 7) = 17/16`
16 (2n2 + 3n ) = 17 ( n2+ 8n + 7)
32n2 + 48n = 17n2+ 136n + 119
32n2 - 17n2 + 48n - 136n - 119 = 0
15n2 - 88n - 119 = 0
Further solving the quadratic equation for n by splitting the middle term, we get,
15n2 - 88n - 119 = 0
15n2 - 105n + 17n +- 119 = 0
15n ( n - 7) + 17 ( n - 7) = 0
( 15n + 17 )(n- 7) = 0
So, we get
15n + 17 = 0
15n = - 17
`n = (-17)/15`
Or
n - 7 = 0
n = 7
Since n is a whole number, it cannot be a fraction. So, n = 7
APPEARS IN
RELATED QUESTIONS
Divide 32 into four parts which are in A.P. such that the product of extremes is to the product of means is 7 : 15.
Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.
Find the sum given below:
`7 + 10 1/2 + 14 + ... + 84`
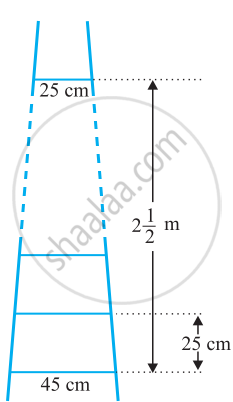
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Find the sum of first 20 terms of the sequence whose nth term is `a_n = An + B`
Choose the correct alternative answer for the following question .
First four terms of an A.P. are ....., whose first term is –2 and common difference is –2.
Choose the correct alternative answer for the following question .
15, 10, 5,... In this A.P sum of first 10 terms is...
If `4/5` , a, 2 are three consecutive terms of an A.P., then find the value of a.
The given terms are 2k + 1, 3k + 3 and 5k − 1. find AP.
The sum of all odd integers between 2 and 100 divisible by 3 is ______.
