Advertisements
Advertisements
Question
If a, b, c, d are in continued proportion, prove that:
(a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc + cd)2.
Solution
L.H.S.
= (d2k6 + d2k4 + d2k2)(d2k4 + d2k2 + d2)
= d2k2 (k4 + k2 + 1)d2 (k4 + k2 + 1)
= d4k2 (k4 + k2 + 1)2
R.H.S.
= (ab + bc + cd)2
= (dk3·dk2 + dk2·dk + dk·d)2
= d4·k2 (k4 + k2 + 1)2
L.H.S. = R.H.S.
Hence proved.
APPEARS IN
RELATED QUESTIONS
If a, b, c are in continued proportion, show that: `(a^2 + b^2)/(b(a + c)) = (b(a + c))/(b^2 + c^2)`.
If a, b, c and d are in proportion prove that `sqrt((4a^2 + 9b^2)/(4c^2 + 9d^2)) = ((xa^3 - 4yb^3)/(xc^3 - 5yd^3))^(1/3)`
Find the third proportional to a2 – b2 and a + b.
The following numbers, K + 3, K + 2, 3K – 7 and 2K – 3 are in proportion. Find K.
If 9, x, x 49 are in proportion, find the value of x.
Find the value of x if 5 : 3 : : x : 6.
35 inland letters cost Rs 87.50. How many such letters can we buy for 315?
The angles of a triangle are in the ratio 3 : 1 : 2. The measure of the largest angle is
10 books is to 15 books as 3 books is to 15 books
Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down.
Unequal masses will balance when the following proportion is true:
`("mass"1)/("length"2) = ("mass"2)/("length"1)`
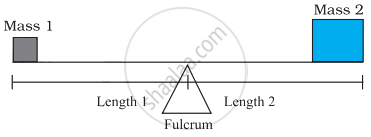
Two children can be balanced on a seesaw when
`("mass"1)/("length"2) = ("mass"2)/("length"1)`. The child on the left and child on the right are balanced. What is the mass of the child on the right?