Advertisements
Advertisements
Question
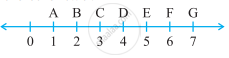
If B is the midpoint of `overline"AC"` and C is the midpoint of `overline"BD"`, where A, B, C, and D lie on a straight line, say why AB = CD?
Solution

Since B is the mid-point of AC,
AB = BC .....(1)
Since C is the mid-point of BD,
BC = CD ....(2)
From equations (1) and (2), we may find that
AB = CD
APPEARS IN
RELATED QUESTIONS
Measure the following line segments.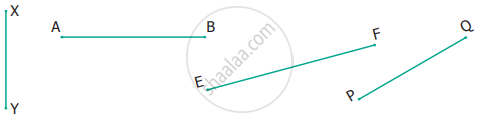
From the given figure, name the
(i) parallel lines
(ii) intersecting lines
(iii) points of intersection.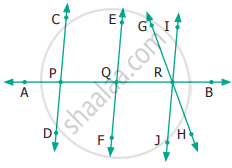
Find the type of lines marked in thick lines
Find the type of lines marked in thick lines
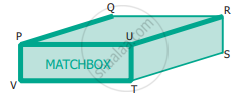
Find the type of lines marked in thick lines
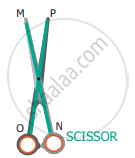
Find the parallel and intersecting line segments in the picture given below.
Why is it better to use a divider than a ruler, while measuring the length of a line segment?
Draw any line segment, say `overline"AB"`. Take any point C lying in between A and B. Measure the lengths of AB, BC, and AC. Is AB = AC + CB?
[Note: If A, B, and C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B.]
If A, B, and C are three points on a line such that AB = 5 cm, BC = 3 cm, and AC = 8 cm, which one of them lies between the other two?
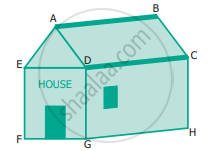
Verify, whether D is the midpoint of `overline"AG"`.