Advertisements
Advertisements
Question
If Points (1, 2) (−5, 6) and (a, −2) are collinear, then a =
Options
−3
7
2
-2
Solution
We have three collinear points A(1,2) ;B(-5,6) ;C(a, - 2).
In general if `A(x_1 ,y_1) ;B(x_2 , y_2) ;C(x_3 ,y_3)` are collinear then,
`x_1(y_2 - y_3 ) + x_2 (y_3 - y_1) + x_3(y_1-y_2) = 0`
So,
1(6 + 2) - 5(- 2-2)+ a (2 -6 ) = 0
So,
-4a + 8 + 20 = 0
Therefore,
a = 7
APPEARS IN
RELATED QUESTIONS
Name the quadrilateral formed, if any, by the following points, and given reasons for your answers:
A(-1,-2) B(1, 0), C (-1, 2), D(-3, 0)
Find the points of trisection of the line segment joining the points:
(3, -2) and (-3, -4)
Find the points of trisection of the line segment joining the points:
(2, -2) and (-7, 4).
Prove that the points (4, 5) (7, 6), (6, 3) (3, 2) are the vertices of a parallelogram. Is it a rectangle.
The line segment joining the points P(3, 3) and Q(6, -6) is trisected at the points A and B such that Ais nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k.
The points A(2, 0), B(9, 1) C(11, 6) and D(4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
The perpendicular distance of the point P (4, 3) from x-axis is
If the point P(x, 3) is equidistant from the point A(7, −1) and B(6, 8), then find the value of x and find the distance AP.
If (a,b) is the mid-point of the line segment joining the points A (10, - 6) , B (k,4) and a - 2b = 18 , find the value of k and the distance AB.
Find the value(s) of k for which the points (3k − 1, k − 2), (k, k − 7) and (k − 1, −k − 2) are collinear.
If the mid-point of the segment joining A (x, y + 1) and B (x + 1, y + 2) is C \[\left( \frac{3}{2}, \frac{5}{2} \right)\] , find x, y.
Write the ratio in which the line segment doining the points A (3, −6), and B (5, 3) is divided by X-axis.
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
Point (0, –7) lies ______.
The point at which the two coordinate axes meet is called the ______.
If y-coordinate of a point is zero, then this point always lies ______.
The point whose ordinate is 4 and which lies on y-axis is ______.
Which of the points P(0, 3), Q(1, 0), R(0, –1), S(–5, 0), T(1, 2) do not lie on the x-axis?
A tiling or tessellation of a flat surface is the covering of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. Historically, tessellations were used in ancient Rome and in Islamic art. You may find tessellation patterns on floors, walls, paintings etc. Shown below is a tiled floor in the archaeological Museum of Seville, made using squares, triangles and hexagons.

A craftsman thought of making a floor pattern after being inspired by the above design. To ensure accuracy in his work, he made the pattern on the Cartesian plane. He used regular octagons, squares and triangles for his floor tessellation pattern
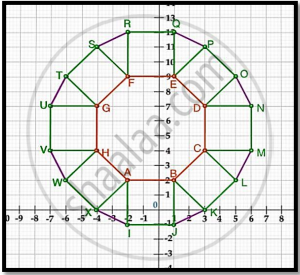
Use the above figure to answer the questions that follow:
- What is the length of the line segment joining points B and F?
- The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the coordinates of Z?
- What are the coordinates of the point on y-axis equidistant from A and G?
OR
What is the area of Trapezium AFGH?
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
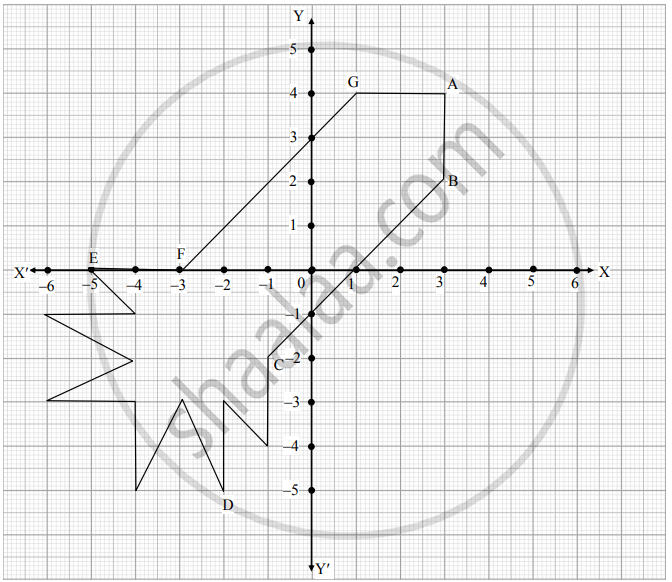
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
