Advertisements
Advertisements
Question
If the product of the roots of the equation `x^2-3x+k=10` is-2 then the value of k is
(a) -2 (b) -8 (c) 8 (d) 12
Solution
(c) 8
It is given that the product of the roots of the equation `x^2-3x+k=10 is -2` . The equation can be rewritten as:
`x^2-3x+(k-10)=0`
Product of the roots of a quadratic equation = `c/a`
⇒` c/a=-2`
⇒ `((k-10))/1=-2`
⇒` k=8`
APPEARS IN
RELATED QUESTIONS
If 1 is a root of the equation `ay^2+ay+3=0` and `y^2+y+b=0` then find the value of ab.
If in an A. P., d = 10, find t6 - t2.
Solve the following quadratic equation :
x2 +8x + 15 = 0
Find c if the system of equations cx+3y+(3 - c ) = 0, 12x + cy - c = 0 has infinitely many solutions?
For the quadratic equation 3x2 + 2x - 1 = 0 , find the value of the discriminant.
Write the degree of Polynomial 5x2 + 2x + 3x4 + 4.
Complete the following activity to form a quadratic equation.
Activity:
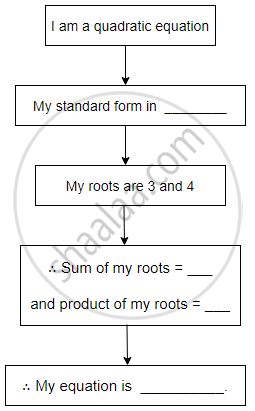
Find c if the system of equations cx + 3y + (3 – c) = 0; 12x + cy – c = 0 has infinitely many solutions?
Solve for x : `1/(2a + b + 2x) =1/(2a) + 1/b + 1/(2x); x ≠ 0, x ≠ (−2a −b)/2`, a, b ≠ 0
In a right-angled triangle, altitude is 2 cm longer than its base. Find the dimensions of the right-angled triangle given that the length of its hypotenuse is 10 cm.
