Advertisements
Advertisements
Question
If in an A. P., d = 10, find t6 - t2.
Options
(A) 10
(B) 20
(c) 30
(D) 40
Solution
(D) 40
APPEARS IN
RELATED QUESTIONS
The sum of the roots of the equation` x^2-6x+2=0`
(a) 2 (b)-2 (c)6 (d)-6
The roots of the equation 2x^2-6x+7=0 are
(a) real, unequal and rational (b) real, unequal and irrational (c) real and equal (d) imaginary
The length of a rectangular field exceeds its breadth by 8 m and the area of the field is `240 m^2` . The breadth of the field is
(a) 20 m (b) 30 m (c) 12 m (d) 16 m
Show the x= -3 is a solution of `x^2+6x+9=0`
Find the value of k so that the quadratic equation` x^2-4kx+k=0`
has equal roots.
Find the value of k for which the quadratic equation `9x^2-3kx+k=0` has equal roots.
Decide whether the following equation is quadratic equation or not.
x2 + 5x – 2 = 0
Decide whether the following equation is quadratic equation or not.
(m + 2) (m – 5) = 0
Product of Pragati’s age 2 years ago and 3 years hence is 84. Find her present age.
Suyash scored 10 marks more in second test than that in the first. 5 times the score of the second test is the same as square of the score in the first test. Find his score in the first test.
Choose the correct answer for the following question.
For \[\sqrt{2} x^2 - 5x + \sqrt{2} = 0\] find the value of the discriminant.
Choose the correct answer for the following question.
Out of the following equations, find the equation having the sum of its roots –5.
Solve the following quadratic equation.
x2 - 4x - 3 = 0
If P(y) = y² - 2y + 5, find P(2) .
Solve the following quadratic equation :
x2 +8x + 15 = 0
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
When the son will be as old as his father today, the sum of their ages then will be 126 years. when the father was as old his son is today. The sum of their ages was 38 years. Find their presents ages.
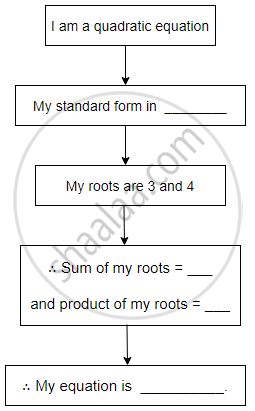
Complete the following activity to form a quadratic equation.
Activity:
Two water taps together can fill a tank in `1(7)/(8)` hours. The tap with longer diameter takes 2 hours less than the tap with a smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
