Advertisements
Advertisements
Question
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Solution
Let the speed of the boat is x km/h in still water
And stream y km/h
According to question,
`30/("x - y") + 44/("x + y") = 10`
And
`40/("x - y") + 55/("x + y") = 13`
Let `1/"x - y" = "u" and 1/"x + y" = "v"`
30u + 44v = 10 ...(i)
40u + 55v = 13 ..(ii)
On solving equation (i) and (ii) we get,
u = `1/5 => "x - y "= 5` ........(iii)
v = `1/11 => "x - y "= 11` ........(iv)
On solving equation (iii) and (iv) we get,
x = 8 km/h
y = 3km/h
APPEARS IN
RELATED QUESTIONS
(a) `3x-x^2=x^2+5` (b) `(x+2)^2=2(x^2-5)`
(c) `(sqrt2x+3)^2=2x^2+6` (d)` (x-1)^2=3x^2+x-2`
The total cost of a certain length of a piece of cloth is Rs 200. If the piece was 5 m longer and each metre of cloth costs Rs 2 less, the cost of the piece would have remained unchanged. How long is the piece and what is its original rate per metre ?
The Sum of squares of 2 consecutive natural even numbers is 244; find the numbers.
Solve the following quadratic equation.
m2 + 5m + 5 = 0
Solve any two of the following.
Solve : `3x+y=14 ; x-y=2`
Write the quadratic equation 7 = 4x - x2 in the form of ax2+bx + c = 0.
Complete the following activity to form a quadratic equation.
Activity:
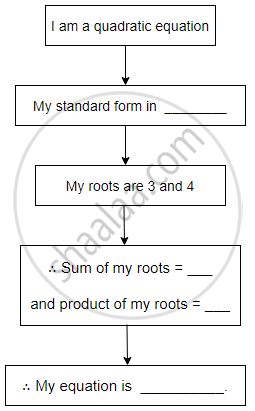
Construct a word problem on quadratic equation, such that one of its answers is 20 (years, rupees, centimeter, etc.). Also, solve it.
Find the value of k for which the quadratic equation kx (x − 2) + 6 = 0 has two equal roots.

In the adjoining fig. `square` ABCD is a trapezium AB || CD and its area is 33 cm2. From the information given in the figure find the lengths of all sides of the `square` ABCD. Fill in the empty boxes to get the solution.
Solution: `square` ABCD is a trapezium.
AB || CD
`"A"(square "ABCD") = 1/2 ("AB" + "CD") xx`______
33 = `1/2 ("x" + 2"x" + 1) xx `______
∴ ______ = (3x + 1) × ______
∴ 3x2 +______ − ______ = 0
∴ 3x(______) + 10(______) = 0
∴ (3x + 10) (______) = 0
∴ (3x + 10) = 0 or ______ = 0
∴ x = `-10/3` or x = ______
But length is never negative.
∴ `"x" ≠ -10/3`
∴ x = ______
AB = ______, CD = ______, AD = BC = ______
