Advertisements
Advertisements
Question
If the sum of first p term of an A.P. is ap2 + bp, find its common difference.
Solution
Here, we are given,
Sp = ap2 + bp
Let us take the first term as a’ and the common difference as d.
Now, as we know,
ap = Sp - Sp -1
So, we get,
`a_p = (ap^2 +bp) - [a(p - 1)^2 + b (p-1)]`
`= ap^2 + bp - [a(p^2 + 1 -2 p) + bp - b] [\text{Using} (a - b)^2 = a^2 + b^2 - ab]`
` = ap^2 + bp - (ap^2 + a - 2ap + bp -b)`
`=ap^2 + bp - ap^2 - a + 2ap - bp +b`
`=2ap - a + b` ..............(1)
Also,
`a_p = a' + (p-1)d`
`= a' + pd - d `
`= pd + ( a' - d)` ..............(2)
On comparing the terms containing p in (1) and (2), we get,
dp = 2ap
d = 2a
Therefore, the common difference is d = 2a .
APPEARS IN
RELATED QUESTIONS
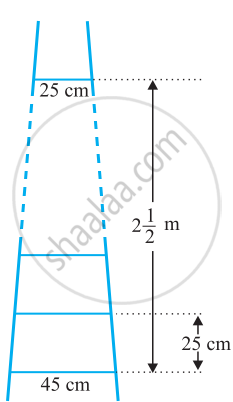
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
If the ratio of the sum of the first n terms of two A.Ps is (7n + 1) : (4n + 27), then find the ratio of their 9th terms.
The sum of n natural numbers is 5n2 + 4n. Find its 8th term.
In an A.P. the first term is 8, nth term is 33 and the sum to first n terms is 123. Find n and d, the common differences.
The sum of first seven terms of an A.P. is 182. If its 4th and the 17th terms are in the ratio 1 : 5, find the A.P.
Write the expression of the common difference of an A.P. whose first term is a and nth term is b.
The first term of an A.P. is p and its common difference is q. Find its 10th term.
If the sum of P terms of an A.P. is q and the sum of q terms is p, then the sum of p + q terms will be
In an A.P. (with usual notations) : given a = 8, an = 62, Sn = 210, find n and d
If the numbers n - 2, 4n - 1 and 5n + 2 are in AP, then the value of n is ______.
