Advertisements
Advertisements
Question
If sum of the number 985 and two other numbers obtained by arranging the digits of 985 in cyclic order is divided by 111, 22 and 37 respectively. Find the quotient in each case.
Solution
\[\text{ The sum of }(985 + 859 + 598)\text{ when divided by }: \]
\[(i) 111\]
\[\text{ Quotient }= (9 + 8 + 5) = 22\]
\[(ii) 22, i . e, (9 + 8 + 5)\]
\[\text{ Quotient }= 111\]
\[(iii) 37 ( = \frac{111}{3})\]
\[\text{ Quotient }= 3(9 + 8 + 5) = 66\]
APPEARS IN
RELATED QUESTIONS
Given an example of a number which is divisible by 4 but not by 8.
Use the same rule to fill the hexagons below.
Now you also make your own magic hexagons.
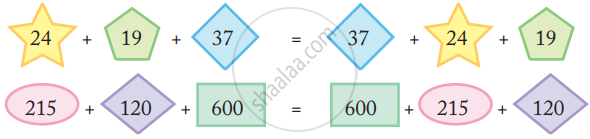
Are they equal?
Now you try and change these numbers into special numbers —
28
Now you try and change these numbers into special numbers —
273
A number is divisible by 11 if the differences between the sum of digits at its odd places and that of digits at the even places is either 0 or divisible by ______.
If A × 3 = 1A, then A = ______.
A five-digit number AABAA is divisible by 33. Write all the numbers of this form.
If 148101B095 is divisible by 33, find the value of B.
If 56 × 32y is divisible by 18, find the least value of y.
