Advertisements
Advertisements
Question
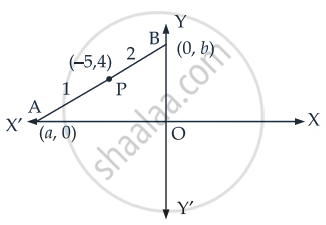
If the intercept of a line between the coordinate axes is divided by the point (–5, 4) in the ratio 1 : 2, then find the equation of the line.
Solution
Let a and b be the intercepts on the given line.
∴ Coordinates of A and B are (a, 0) and (0, b) respectively
∴ – 5 = `(1 xx 0 + 2 xx a)/(1 + 2)`
⇒ 2a = – 15 .......`[(because "X" = (m_1x_2 + m_2x_1)/(m_1 + m_2)),("and" "Y" = (m_1y_2 + m_2y_1)/(m_1 + m_2))]`
⇒ a = ` (-15)/2`
∴ A = `((-15)/2, 0)`
And 4 = `(1 xx b + 0 xx 2)/(1 + 2)`
⇒ 4 = `b/3`
⇒ b = 12
∴ B = (0, 12)
So, the equation of line AB is
y – y1 = `(y_2 - y_1)/(x_2 - x_1) (x - x_1)`
y – 0 = `((12 - 0)/(0 + 15/2)) (x + 15/2)`
⇒ y = `(12 xx 2)/15 (x + 15/2)`
⇒ y = `8/5(x + 15/2)`
⇒ 5y = 8x + 60
⇒ 8x – 5y + 60 = 0
Hence, the required equation is 8x – 5y + 60 = 0.
APPEARS IN
RELATED QUESTIONS
Reduce the following equation into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
`x – sqrt3y + 8 = 0`
Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (–2, 3).
Find angles between the lines `sqrt3x + y = 1 and x + sqrt3y = 1`.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
Show that the equation of the line passing through the origin and making an angle θ with the line `y = mx + c " is " y/c = (m+- tan theta)/(1 +- m tan theta)`.
Find the equation of a line making an angle of 150° with the x-axis and cutting off an intercept 2 from y-axis.
Find the equation of the right bisector of the line segment joining the points A (1, 0) and B (2, 3).
Point R (h, k) divides a line segment between the axes in the ratio 1 : 2. Find the equation of the line.
Find the equation of a line for p = 4, α = 150°.
Find the equation of the straight line on which the length of the perpendicular from the origin is 2 and the perpendicular makes an angle α with x-axis such that sin α = \[\frac{1}{3}\].
Reduce the following equation to the normal form and find p and α in \[x + \sqrt{3}y - 4 = 0\] .
Reduce the lines 3 x − 4 y + 4 = 0 and 2 x + 4 y − 5 = 0 to the normal form and hence find which line is nearer to the origin.
Find the area of the triangle formed by the line x + y − 6 = 0, x − 3y − 2 = 0 and 5x − 3y + 2 = 0.
Prove that the lines \[y = \sqrt{3}x + 1, y = 4 \text { and } y = - \sqrt{3}x + 2\] form an equilateral triangle.
Find the orthocentre of the triangle the equations of whose sides are x + y = 1, 2x + 3y = 6 and 4x − y + 4 = 0.
If a, b, c are in A.P., prove that the straight lines ax + 2y + 1 = 0, bx + 3y + 1 = 0 and cx + 4y + 1 = 0 are concurrent.
Find the image of the point (2, 1) with respect to the line mirror x + y − 5 = 0.
Find the values of α so that the point P (α2, α) lies inside or on the triangle formed by the lines x − 5y+ 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0.
Determine whether the point (−3, 2) lies inside or outside the triangle whose sides are given by the equations x + y − 4 = 0, 3x − 7y + 8 = 0, 4x − y − 31 = 0 .
The point which divides the join of (1, 2) and (3, 4) externally in the ratio 1 : 1
If the lines ax + 12y + 1 = 0, bx + 13y + 1 = 0 and cx + 14y + 1 = 0 are concurrent, then a, b, c are in
Find the equation of a line which passes through the point (2, 3) and makes an angle of 30° with the positive direction of x-axis.
The inclination of the line x – y + 3 = 0 with the positive direction of x-axis is ______.
If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be ______.
The line which cuts off equal intercept from the axes and pass through the point (1, –2) is ______.
Reduce the following equation into slope-intercept form and find their slopes and the y-intercepts.
6x + 3y – 5 = 0
Reduce the following equation into intercept form and find their intercepts on the axes.
4x – 3y = 6
