Advertisements
Advertisements
Question
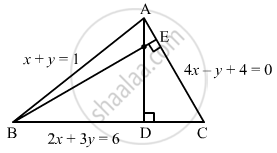
Find the orthocentre of the triangle the equations of whose sides are x + y = 1, 2x + 3y = 6 and 4x − y + 4 = 0.
Solution
The given lines are as follows:
x + y = 1 ... (1)
2x + 3y = 6 ... (2)
4x − y + 4 = 0 ... (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x = −3, y = 4
Thus, AB and BC intersect at B (−3, 4).
Solving (1) and (3):
x = \[- \frac{3}{5}\] , y = \[\frac{8}{5}\]
Thus, AB and CA intersect at
\[A \left( - \frac{3}{5}, \frac{8}{5} \right)\].
Let AD and BE be the altitudes.
\[AD \perp BC \text { and }BE \perp AC\]
\[\therefore\] Slope of AD \[\times\] Slope of BC = −1
and Slope of BE \[\times\] Slope of AC = −1
Here, slope of BC = slope of the line (2) = \[- \frac{2}{3}\] and slope of AC = slope of the line (3) = 4
\[\therefore \text { Slope of AD } \times \left( - \frac{2}{3} \right) = - 1 \text { and slope of BE } \times 4 = - 1\]
\[ \Rightarrow \text { Slope of AD } = \frac{3}{2} \text { and slope of BE } = - \frac{1}{4}\]
The equation of the altitude AD passing through \[A \left( - \frac{3}{5}, \frac{8}{5} \right)\] and having slope \[\frac{3}{2}\] is \[y - \frac{8}{5} = \frac{3}{2}\left( x + \frac{3}{5} \right)\]
\[\Rightarrow 3x - 2y + 5 = 0\] ... (4)
The equation of the altitude BE passing through B (−3, 4) and having slope \[- \frac{1}{4}\] is \[y - 4 = - \frac{1}{4}\left( x + 3 \right)\]
\[\Rightarrow x + 4y - 13 = 0\] ... (5)
Solving (4) and (5), we get
\[\left( \frac{3}{7}, \frac{22}{7} \right)\] as the orthocentre of the triangle.
APPEARS IN
RELATED QUESTIONS
Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (–2, 3).
Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A (x –x1) + B (y – y1) = 0.
Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2, find equation of the other line.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).
The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.
If p and q are the lengths of perpendiculars from the origin to the lines x cos θ – y sin θ = k cos 2θ and xsec θ+ y cosec θ = k, respectively, prove that p2 + 4q2 = k2.
Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Find the equation of a line which makes an angle of tan−1 (3) with the x-axis and cuts off an intercept of 4 units on negative direction of y-axis.
Find the lines through the point (0, 2) making angles \[\frac{\pi}{3} \text { and } \frac{2\pi}{3}\] with the x-axis. Also, find the lines parallel to them cutting the y-axis at a distance of 2 units below the origin.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (−1, 2).
Find the equation of the right bisector of the line segment joining the points A (1, 0) and B (2, 3).
Find the equations of the sides of the triangles the coordinates of whose angular point is respectively (1, 4), (2, −3) and (−1, −2).
Find the equation of the side BC of the triangle ABC whose vertices are (−1, −2), (0, 1) and (2, 0) respectively. Also, find the equation of the median through (−1, −2).
Find the equation of the line on which the length of the perpendicular segment from the origin to the line is 4 and the inclination of the perpendicular segment with the positive direction of x-axis is 30°.
The length of the perpendicular from the origin to a line is 7 and the line makes an angle of 150° with the positive direction of Y-axis. Find the equation of the line.
Reduce the following equation to the normal form and find p and α in \[x - y + 2\sqrt{2} = 0\].
Put the equation \[\frac{x}{a} + \frac{y}{b} = 1\] to the slope intercept form and find its slope and y-intercept.
Find the point of intersection of the following pairs of lines:
2x − y + 3 = 0 and x + y − 5 = 0
Find the point of intersection of the following pairs of lines:
bx + ay = ab and ax + by = ab.
Find the coordinates of the vertices of a triangle, the equations of whose sides are x + y − 4 = 0, 2x − y + 3 = 0 and x − 3y + 2 = 0.
Find the area of the triangle formed by the line y = m1 x + c1, y = m2 x + c2 and x = 0.
Prove that the lines \[y = \sqrt{3}x + 1, y = 4 \text { and } y = - \sqrt{3}x + 2\] form an equilateral triangle.
Prove that the following sets of three lines are concurrent:
3x − 5y − 11 = 0, 5x + 3y − 7 = 0 and x + 2y = 0
Prove that the following sets of three lines are concurrent:
\[\frac{x}{a} + \frac{y}{b} = 1, \frac{x}{b} + \frac{y}{a} = 1\text { and } y = x .\]
Show that the straight lines L1 = (b + c) x + ay + 1 = 0, L2 = (c + a) x + by + 1 = 0 and L3 = (a + b) x + cy + 1 = 0 are concurrent.
If a, b, c are in A.P., prove that the straight lines ax + 2y + 1 = 0, bx + 3y + 1 = 0 and cx + 4y + 1 = 0 are concurrent.
Find the equation of the straight line perpendicular to 2x − 3y = 5 and cutting off an intercept 1 on the positive direction of the x-axis.
Find the equation of the straight line which has y-intercept equal to \[\frac{4}{3}\] and is perpendicular to 3x − 4y + 11 = 0.
Find the equation of the right bisector of the line segment joining the points (a, b) and (a1, b1).
Find the projection of the point (1, 0) on the line joining the points (−1, 2) and (5, 4).
Determine whether the point (−3, 2) lies inside or outside the triangle whose sides are given by the equations x + y − 4 = 0, 3x − 7y + 8 = 0, 4x − y − 31 = 0 .
Write the coordinates of the orthocentre of the triangle formed by the lines xy = 0 and x + y = 1.
The centroid of a triangle is (2, 7) and two of its vertices are (4, 8) and (−2, 6). The third vertex is
Find the equation of the line which passes through the point (– 4, 3) and the portion of the line intercepted between the axes is divided internally in the ratio 5 : 3 by this point.
If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be ______.
Locus of the mid-points of the portion of the line x sin θ + y cos θ = p intercepted between the axes is ______.
Reduce the following equation into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
y − 2 = 0
