Advertisements
Advertisements
Question
Locus of the mid-points of the portion of the line x sin θ + y cos θ = p intercepted between the axes is ______.
Solution
Locus of the mid-points of the portion of the line x sin θ + y cos θ = p intercepted between the axes is 4x2y2 = p2(x2 + y2).
Explanation:
Given equation of the line is
x cos θ + y sin θ = p ......(i)
Let C(h, k) be the mid-point of the given line AB where it meets the two-axis at A(a, 0) and B(0, b).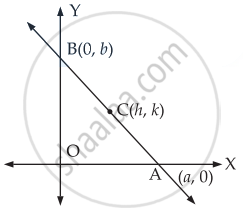
Since (a, 0) lies on equation (i) then
a cos θ + 0 = p
⇒ `a = p/costheta` ......(ii)
B(0, b) also lies on the equation (i) then
0 + b sin θ = p
⇒ `b = p/sintheta` ......(iii)
Since C(h, k) is the mid-point of AB
∴ `h = (0 + a)/2`
⇒ a = 2h
And k = `(b + 0)/2`
⇒ b = 2k
Putting the values of a and b is equation (ii) and (iii) we get
2h = `p/costheta`
⇒ cos θ = `p/(2h)` ......(iv)
And 2h = `p/sintheta`
⇒ sin θ = `p/(2k)` ......(v)
Squaring and adding equation (iv) and (v) we get
⇒ cos2θ + sin2θ = `p^2/(4h^2) + p^2/(4k^2)`
⇒ 1 = `p^2/(4h^2) + p^2/(4k^2)`
So, the locus of the mid-point is
1 = `p^2/(4x^2) + p^2/(4y^2)`
⇒ 4x2y2 = p2(x2 + y2)
APPEARS IN
RELATED QUESTIONS
Show that the equation of the line passing through the origin and making an angle θ with the line `y = mx + c " is " y/c = (m+- tan theta)/(1 +- m tan theta)`.
Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Find the equation of a line making an angle of 150° with the x-axis and cutting off an intercept 2 from y-axis.
Find the equation of the bisector of angle A of the triangle whose vertices are A (4, 3), B (0, 0) and C(2, 3).
Point R (h, k) divides a line segment between the axes in the ratio 1 : 2. Find the equation of the line.
Find the equation of a line for p = 5, α = 60°.
Find the value of θ and p, if the equation x cos θ + y sin θ = p is the normal form of the line \[\sqrt{3}x + y + 2 = 0\].
Reduce the following equation to the normal form and find p and α in \[x + \sqrt{3}y - 4 = 0\] .
Put the equation \[\frac{x}{a} + \frac{y}{b} = 1\] to the slope intercept form and find its slope and y-intercept.
Find the point of intersection of the following pairs of lines:
bx + ay = ab and ax + by = ab.
Find the area of the triangle formed by the line y = m1 x + c1, y = m2 x + c2 and x = 0.
Prove that the lines \[y = \sqrt{3}x + 1, y = 4 \text { and } y = - \sqrt{3}x + 2\] form an equilateral triangle.
Find the conditions that the straight lines y = m1 x + c1, y = m2 x + c2 and y = m3 x + c3 may meet in a point.
If the lines p1 x + q1 y = 1, p2 x + q2 y = 1 and p3 x + q3 y = 1 be concurrent, show that the points (p1, q1), (p2, q2) and (p3, q3) are collinear.
Show that the straight lines L1 = (b + c) x + ay + 1 = 0, L2 = (c + a) x + by + 1 = 0 and L3 = (a + b) x + cy + 1 = 0 are concurrent.
Find the equation of the straight line perpendicular to 2x − 3y = 5 and cutting off an intercept 1 on the positive direction of the x-axis.
Find the equation of the straight line which has y-intercept equal to \[\frac{4}{3}\] and is perpendicular to 3x − 4y + 11 = 0.
Find the values of α so that the point P (α2, α) lies inside or on the triangle formed by the lines x − 5y+ 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0.
Find the values of the parameter a so that the point (a, 2) is an interior point of the triangle formed by the lines x + y − 4 = 0, 3x − 7y − 8 = 0 and 4x − y − 31 = 0.
Write the coordinates of the orthocentre of the triangle formed by the lines x2 − y2 = 0 and x + 6y = 18.
Find the equation of the line where length of the perpendicular segment from the origin to the line is 4 and the inclination of the perpendicular segment with the positive direction of x-axis is 30°.
A line passes through P(1, 2) such that its intercept between the axes is bisected at P. The equation of the line is ______.
Find the equation of the lines which passes through the point (3, 4) and cuts off intercepts from the coordinate axes such that their sum is 14.
If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be ______.
Reduce the following equation into intercept form and find their intercepts on the axes.
4x – 3y = 6
Reduce the following equation into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
x − y = 4
