Advertisements
Advertisements
प्रश्न
Locus of the mid-points of the portion of the line x sin θ + y cos θ = p intercepted between the axes is ______.
उत्तर
Locus of the mid-points of the portion of the line x sin θ + y cos θ = p intercepted between the axes is 4x2y2 = p2(x2 + y2).
Explanation:
Given equation of the line is
x cos θ + y sin θ = p ......(i)
Let C(h, k) be the mid-point of the given line AB where it meets the two-axis at A(a, 0) and B(0, b).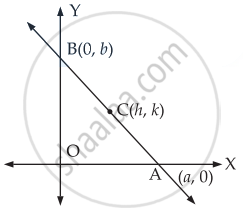
Since (a, 0) lies on equation (i) then
a cos θ + 0 = p
⇒ `a = p/costheta` ......(ii)
B(0, b) also lies on the equation (i) then
0 + b sin θ = p
⇒ `b = p/sintheta` ......(iii)
Since C(h, k) is the mid-point of AB
∴ `h = (0 + a)/2`
⇒ a = 2h
And k = `(b + 0)/2`
⇒ b = 2k
Putting the values of a and b is equation (ii) and (iii) we get
2h = `p/costheta`
⇒ cos θ = `p/(2h)` ......(iv)
And 2h = `p/sintheta`
⇒ sin θ = `p/(2k)` ......(v)
Squaring and adding equation (iv) and (v) we get
⇒ cos2θ + sin2θ = `p^2/(4h^2) + p^2/(4k^2)`
⇒ 1 = `p^2/(4h^2) + p^2/(4k^2)`
So, the locus of the mid-point is
1 = `p^2/(4x^2) + p^2/(4y^2)`
⇒ 4x2y2 = p2(x2 + y2)
APPEARS IN
संबंधित प्रश्न
Find angles between the lines `sqrt3x + y = 1 and x + sqrt3y = 1`.
Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A (x –x1) + B (y – y1) = 0.
If p and q are the lengths of perpendiculars from the origin to the lines x cos θ – y sin θ = k cos 2θ and xsec θ+ y cosec θ = k, respectively, prove that p2 + 4q2 = k2.
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and –6, respectively.
Find the equation of a line for p = 5, α = 60°.
Find the equation of a line for p = 8, α = 300°.
Find the equation of the straight line on which the length of the perpendicular from the origin is 2 and the perpendicular makes an angle α with x-axis such that sin α = \[\frac{1}{3}\].
The length of the perpendicular from the origin to a line is 7 and the line makes an angle of 150° with the positive direction of Y-axis. Find the equation of the line.
Find the equation of a straight line on which the perpendicular from the origin makes an angle of 30° with x-axis and which forms a triangle of area \[50/\sqrt{3}\] with the axes.
If the straight line through the point P (3, 4) makes an angle π/6 with the x-axis and meets the line 12x + 5y + 10 = 0 at Q, find the length PQ.
Reduce the equation \[\sqrt{3}\] x + y + 2 = 0 to the normal form and find p and α.
Find the coordinates of the vertices of a triangle, the equations of whose sides are
y (t1 + t2) = 2x + 2a t1t2, y (t2 + t3) = 2x + 2a t2t3 and, y (t3 + t1) = 2x + 2a t1t3.
Find the coordinates of the incentre and centroid of the triangle whose sides have the equations 3x− 4y = 0, 12y + 5x = 0 and y − 15 = 0.
Prove that the following sets of three lines are concurrent:
3x − 5y − 11 = 0, 5x + 3y − 7 = 0 and x + 2y = 0
If the lines p1 x + q1 y = 1, p2 x + q2 y = 1 and p3 x + q3 y = 1 be concurrent, show that the points (p1, q1), (p2, q2) and (p3, q3) are collinear.
Show that the straight lines L1 = (b + c) x + ay + 1 = 0, L2 = (c + a) x + by + 1 = 0 and L3 = (a + b) x + cy + 1 = 0 are concurrent.
Find the projection of the point (1, 0) on the line joining the points (−1, 2) and (5, 4).
Find the values of α so that the point P (α2, α) lies inside or on the triangle formed by the lines x − 5y+ 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0.
Write the coordinates of the orthocentre of the triangle formed by the lines x2 − y2 = 0 and x + 6y = 18.
If a ≠ b ≠ c, write the condition for which the equations (b − c) x + (c − a) y + (a − b) = 0 and (b3 − c3) x + (c3 − a3) y + (a3 − b3) = 0 represent the same line.
The equations of the sides AB, BC and CA of ∆ ABC are y − x = 2, x + 2y = 1 and 3x + y + 5 = 0 respectively. The equation of the altitude through B is
Prove that every straight line has an equation of the form Ax + By + C = 0, where A, B and C are constants.
The inclination of the line x – y + 3 = 0 with the positive direction of x-axis is ______.
A line passes through P(1, 2) such that its intercept between the axes is bisected at P. The equation of the line is ______.
Find the equation of the straight line which passes through the point (1, – 2) and cuts off equal intercepts from axes.
A line cutting off intercept – 3 from the y-axis and the tangent at angle to the x-axis is `3/5`, its equation is ______.
The line which cuts off equal intercept from the axes and pass through the point (1, –2) is ______.
