Question

Find the values of the parameter a so that the point (a, 2) is an interior point of the triangle formed by the lines x + y − 4 = 0, 3x − 7y − 8 = 0 and 4x − y − 31 = 0.

Answer 1

Let ABC be the triangle of sides AB, BC and CA whose equations are  x + y − 4 = 0, 3x − 7y − 8 = 0 and 4x − y − 31 = 0, respectively.
On solving them, we get

\[A \left( 7, - 3 \right)\],

\[B \left( \frac{18}{5}, \frac{2}{5} \right)\]  and \[C \left( \frac{209}{25}, \frac{61}{25} \right)\]  as the coordinates of the vertices.
Let P (a, 2) be the given point.

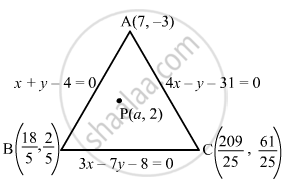
It is given that point P (a,2) lies inside the triangle. So, we have the following:
(i) A and P must lie on the same side of BC.
(ii) B and P must lie on the same side of AC.
(iii) C and P must lie on the same side of AB.
Thus, if A and P lie on the same side of BC, then \[\left( 21 + 21 - 8 \right)\left( 3a - 14 - 8 \right) > 0\]

\[\Rightarrow a > \frac{22}{3}\]         ... (1)

If B and P lie on the same side of AC, then \[\left( \frac{4 \times 18}{5} - \frac{2}{5} - 31 \right)\left( 4a - 2 - 31 \right) > 0\] 

\[\Rightarrow a < \frac{33}{4}\]       ... (2)

If C and P lie on the same side of AB, then

\[\left( \frac{209}{25} + \frac{61}{25} - 4 \right)\left( a + 2 - 4 \right) > 0\]

\[ \Rightarrow \left( \frac{34}{5} - 4 \right)\left( a + 2 - 4 \right) > 0\]

\[\Rightarrow a > 2\]       ... (3)
From (1), (2) and (3), we get:

\[a \in \left( \frac{22}{3}, \frac{33}{4} \right)\]