Question

Find the equation of a straight line on which the perpendicular from the origin makes an angle of 30° with x-axis and which forms a triangle of area \[50/\sqrt{3}\] with the axes.

Answer 1

Let AB be the given line and OL = p be the perpendicular drawn from the origin on the line.

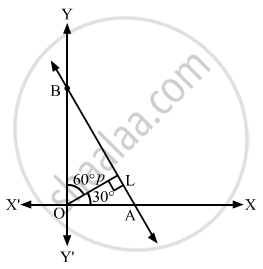
Here,

\[\alpha = {30}^\circ\]

So, the equation of the line AB is

\[xcos\alpha + ysin\alpha = p \]

\[ \Rightarrow x\cos {30}^\circ + y\sin {30}^\circ = p\]

\[ \Rightarrow \frac{\sqrt{3}x}{2} + \frac{y}{2} = p\]

\[ \Rightarrow \sqrt{3}x + y = 2p . . . (1)\]

Now, in triangles OLA and OLB

\[\cos {30}^\circ = \frac{OL}{OA}\text {  and } \cos {60}^\circ = \frac{OL}{OB}\]

\[ \Rightarrow \frac{\sqrt{3}}{2} = \frac{p}{OA} \text { and }\frac{1}{2} = \frac{p}{OB}\]

\[ \Rightarrow OA = \frac{2p}{\sqrt{3}} \text { and} OB = 2p\]

It is given that the area of triangle OAB is \[50/\sqrt{3}\]

\[\therefore \frac{1}{2} \times OA \times OB = \frac{50}{\sqrt{3}}\]

\[ \Rightarrow \frac{1}{2} \times \frac{2p}{\sqrt{3}} \times 2p = \frac{50}{\sqrt{3}}\]

\[ \Rightarrow p^2 = 25\]

\[ \Rightarrow p = 5\]

Substituting the value of p in (1):

\[\sqrt{3}x + y = 10\]

Hence, the equation of the line AB is

\[x + \sqrt{3}y = 10\].