Advertisements
Advertisements
Question
Find the coordinates of the incentre and centroid of the triangle whose sides have the equations 3x− 4y = 0, 12y + 5x = 0 and y − 15 = 0.
Solution
The given lines are as follows:
3x − 4y = 0 ... (1)
12y + 5x = 0 ... (2)
y − 15 = 0 ... (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
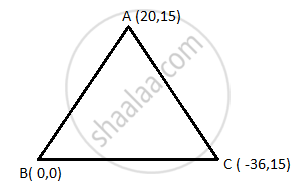
Solving (1) and (2):
x = 0, y = 0
Thus, AB and BC intersect at B (0, 0).
Solving (1) and (3):
x = 20 , y = 15
Thus, AB and CA intersect at A (20, 15).
Solving (2) and (3):
x = −36 , y = 15
Thus, BC and CA intersect at C (−36, 15).
Let us find the lengths of sides AB, BC and CA.
\[AB = \sqrt{\left( 20 - 0 \right)^2 + \left( 15 - 0 \right)^2} = 25\]
\[BC = \sqrt{\left( 0 + 36 \right)^2 + \left( 0 - 15 \right)^2} = 39\]
\[AC = \sqrt{\left( 20 + 36 \right)^2 + \left( 15 - 15 \right)^2} = 56\]
Here, a = BC = 39, b = CA = 56 and c = AB = 25
Also,
\[\left( x_1 , y_1 \right)\] = A (20, 15), \[\left( x_2 , y_2 \right)\] = B (0, 0) and \[\left( x_3 , y_3 \right)\] = C (−36, 15)
\[\therefore\text{ Centroid }= \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)\]
\[ = \left( \frac{20 + 0 - 36}{3}, \frac{15 + 0 + 15}{3} \right) = \left( \frac{- 16}{3}, 10 \right)\]
\[\text { And, incentre } = \left( \frac{a x_1 + b x_2 + c x_3}{a + b + c}, \frac{a y_1 + b y_2 + c y_3}{a + b + c} \right)\]
\[ = \left( \frac{39 \times 20 + 56 \times 0 - 25 \times 36}{39 + 56 + 25}, \frac{39 \times 15 + 56 \times 0 + 25 \times 15}{39 + 56 + 25} \right)\]
\[ = \left( \frac{- 120}{120}, \frac{120 \times 8}{120} \right) = \left( - 1, 8 \right)\]
APPEARS IN
RELATED QUESTIONS
Find angles between the lines `sqrt3x + y = 1 and x + sqrt3y = 1`.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).
The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
Find the equation of a line making an angle of 150° with the x-axis and cutting off an intercept 2 from y-axis.
Find the equation of a line that has y-intercept −4 and is parallel to the line joining (2, −5) and (1, 2).
Find the lines through the point (0, 2) making angles \[\frac{\pi}{3} \text { and } \frac{2\pi}{3}\] with the x-axis. Also, find the lines parallel to them cutting the y-axis at a distance of 2 units below the origin.
Find the equations of the sides of the triangles the coordinates of whose angular point is respectively (1, 4), (2, −3) and (−1, −2).
Find the equations of the diagonals of the square formed by the lines x = 0, y = 0, x = 1 and y =1.
Find the equation of the straight line on which the length of the perpendicular from the origin is 2 and the perpendicular makes an angle α with x-axis such that sin α = \[\frac{1}{3}\].
The length of the perpendicular from the origin to a line is 7 and the line makes an angle of 150° with the positive direction of Y-axis. Find the equation of the line.
Reduce the equation \[\sqrt{3}\] x + y + 2 = 0 to slope-intercept form and find slope and y-intercept;
Put the equation \[\frac{x}{a} + \frac{y}{b} = 1\] to the slope intercept form and find its slope and y-intercept.
Find the area of the triangle formed by the line y = 0, x = 2 and x + 2y = 3.
Find the area of the triangle formed by the line x + y − 6 = 0, x − 3y − 2 = 0 and 5x − 3y + 2 = 0.
Prove that the lines \[y = \sqrt{3}x + 1, y = 4 \text { and } y = - \sqrt{3}x + 2\] form an equilateral triangle.
Find the orthocentre of the triangle the equations of whose sides are x + y = 1, 2x + 3y = 6 and 4x − y + 4 = 0.
Prove that the following sets of three lines are concurrent:
15x − 18y + 1 = 0, 12x + 10y − 3 = 0 and 6x + 66y − 11 = 0
Prove that the following sets of three lines are concurrent:
3x − 5y − 11 = 0, 5x + 3y − 7 = 0 and x + 2y = 0
Find the equation of the right bisector of the line segment joining the points (a, b) and (a1, b1).
Find the image of the point (2, 1) with respect to the line mirror x + y − 5 = 0.
If the image of the point (2, 1) with respect to the line mirror be (5, 2), find the equation of the mirror.
Find the coordinates of the foot of the perpendicular from the point (−1, 3) to the line 3x − 4y − 16 = 0.
Find the projection of the point (1, 0) on the line joining the points (−1, 2) and (5, 4).
Find the values of α so that the point P (α2, α) lies inside or on the triangle formed by the lines x − 5y+ 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0.
Find the values of the parameter a so that the point (a, 2) is an interior point of the triangle formed by the lines x + y − 4 = 0, 3x − 7y − 8 = 0 and 4x − y − 31 = 0.
If a ≠ b ≠ c, write the condition for which the equations (b − c) x + (c − a) y + (a − b) = 0 and (b3 − c3) x + (c3 − a3) y + (a3 − b3) = 0 represent the same line.
Two vertices of a triangle are (−2, −1) and (3, 2) and third vertex lies on the line x + y = 5. If the area of the triangle is 4 square units, then the third vertex is
A point equidistant from the line 4x + 3y + 10 = 0, 5x − 12y + 26 = 0 and 7x+ 24y − 50 = 0 is
Find the equation of the line where length of the perpendicular segment from the origin to the line is 4 and the inclination of the perpendicular segment with the positive direction of x-axis is 30°.
Find the equation of the straight line which passes through the point (1, – 2) and cuts off equal intercepts from axes.
For what values of a and b the intercepts cut off on the coordinate axes by the line ax + by + 8 = 0 are equal in length but opposite in signs to those cut off by the line 2x – 3y + 6 = 0 on the axes.
A line cutting off intercept – 3 from the y-axis and the tangent at angle to the x-axis is `3/5`, its equation is ______.
If the line `x/"a" + y/"b"` = 1 passes through the points (2, –3) and (4, –5), then (a, b) is ______.
