Advertisements
Advertisements
Question
Three sides AB, BC and CA of a triangle ABC are 5x − 3y + 2 = 0, x − 3y − 2 = 0 and x + y − 6 = 0 respectively. Find the equation of the altitude through the vertex A.
Solution
The sides AB, BC and CA of a triangle ABC are as follows:
5x − 3y + 2 = 0 ... (1)
x − 3y − 2 = 0 ... (2)
x + y − 6 = 0 ... (3)
Solving (1) and (3):
x = 2 , y = 4
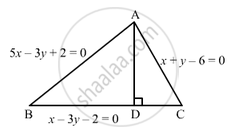
Thus, AB and CA intersect at A (2, 4).
Let AD be the altitude.
\[AD \perp BC\]
\[\therefore\] Slope of AD \[\times\] Slope of BC = −1
Here, slope of BC = slope of the line (2) = \[\frac{1}{3}\]
\[\therefore \text { Slope of AD }\times \frac{1}{3} = - 1 \]
\[ \Rightarrow \text { Slope of AD } = - 3\]
Hence, the equation of the altitude AD passing through A (2, 4) and having slope −3 is
\[y - 4 = - 3\left( x - 2 \right)\]
\[ \Rightarrow 3x + y = 10\]
APPEARS IN
RELATED QUESTIONS
Find the equation of the line parallel to x-axis and passing through (3, −5).
Find the equation of a line equidistant from the lines y = 10 and y = − 2.
Find the equation of the straight line passing through the point (6, 2) and having slope − 3.
Find the equation of the straight line passing through (−2, 3) and inclined at an angle of 45° with the x-axis.
Find the equation of the line passing through \[(2, 2\sqrt{3})\] and inclined with x-axis at an angle of 75°.
Find the equation of the straight line which divides the join of the points (2, 3) and (−5, 8) in the ratio 3 : 4 and is also perpendicular to it.
Find the equation of the line passing through the point (−3, 5) and perpendicular to the line joining (2, 5) and (−3, 6).
Find the equation of the straight lines passing through the following pair of point :
(0, 0) and (2, −2)
Find the equation of the straight lines passing through the following pair of point :
(0, −a) and (b, 0)
Find the equations to the diagonals of the rectangle the equations of whose sides are x = a, x = a', y= b and y = b'.
Find the equation to the straight line cutting off intercepts 3 and 2 from the axes.
Find the equation to the straight line which cuts off equal positive intercepts on the axes and their product is 25.
Find the equation of the line which passes through the point (− 4, 3) and the portion of the line intercepted between the axes is divided internally in the ratio 5 : 3 by this point.
Find the equation of the straight line which passes through the point P (2, 6) and cuts the coordinate axes at the point A and B respectively so that \[\frac{AP}{BP} = \frac{2}{3}\] .
Find the equations of the straight lines each of which passes through the point (3, 2) and cuts off intercepts a and b respectively on X and Y-axes such that a − b = 2.
Find the equation of the straight line passing through the origin and bisecting the portion of the line ax + by + c = 0 intercepted between the coordinate axes.
Find the equation of straight line passing through (−2, −7) and having an intercept of length 3 between the straight lines 4x + 3y = 12 and 4x + 3y = 3.
Find the equation of a line passing through (3, −2) and perpendicular to the line x − 3y + 5 = 0.
Find the equation of the straight line through the point (α, β) and perpendicular to the line lx + my + n = 0.
Find the distance of the point (1, 2) from the straight line with slope 5 and passing through the point of intersection of x + 2y = 5 and x − 3y = 7.
Find the equation of the straight lines passing through the origin and making an angle of 45° with the straight line \[\sqrt{3}x + y = 11\].
Find the equations to the straight lines which pass through the origin and are inclined at an angle of 75° to the straight line \[x + y + \sqrt{3}\left( y - x \right) = a\].
Find the equations of two straight lines passing through (1, 2) and making an angle of 60° with the line x + y = 0. Find also the area of the triangle formed by the three lines.
Find the equation of the straight line drawn through the point of intersection of the lines x + y = 4 and 2x − 3y = 1 and perpendicular to the line cutting off intercepts 5, 6 on the axes.
Show that the straight lines given by (2 + k) x + (1 + k) y = 5 + 7k for different values of k pass through a fixed point. Also, find that point.
Write the integral values of m for which the x-coordinate of the point of intersection of the lines y = mx + 1 and 3x + 4y = 9 is an integer.
If a, b, c are in G.P. write the area of the triangle formed by the line ax + by + c = 0 with the coordinates axes.
The equation of the straight line which passes through the point (−4, 3) such that the portion of the line between the axes is divided internally by the point in the ratio 5 : 3 is
If a + b + c = 0, then the family of lines 3ax + by + 2c = 0 pass through fixed point
The inclination of the straight line passing through the point (−3, 6) and the mid-point of the line joining the point (4, −5) and (−2, 9) is
Find the equation of lines passing through (1, 2) and making angle 30° with y-axis.
Find the equation of the line passing through the point of intersection of 2x + y = 5 and x + 3y + 8 = 0 and parallel to the line 3x + 4y = 7.
In what direction should a line be drawn through the point (1, 2) so that its point of intersection with the line x + y = 4 is at a distance `sqrt(6)/3` from the given point.
If a, b, c are in A.P., then the straight lines ax + by + c = 0 will always pass through ______.
The straight line 5x + 4y = 0 passes through the point of intersection of the straight lines x + 2y – 10 = 0 and 2x + y + 5 = 0.
The lines ax + 2y + 1 = 0, bx + 3y + 1 = 0 and cx + 4y + 1 = 0 are concurrent if a, b, c are in G.P.
