Question

Find the equations of two straight lines passing through (1, 2) and making an angle of 60° with the line x + y = 0. Find also the area of the triangle formed by the three lines.

Answer 1

Let A(1, 2) be the vertex of the triangle ABC and x + y = 0 be the equation of BC.

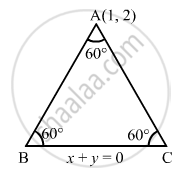
Here, we have to find the equations of sides AB and AC, each of which makes an angle of $${60}^{\circ }$$ with the line x + y = 0.

We know the equations of two lines passing through a point $$(x_1,y_1)$$ and making an angle $$\alpha$$ with the line whose slope is m. 

$$y-y_1=\frac{m\pm \tan \alpha }{1\mp m\tan \alpha }(x-x_1)$$

Here, 

$$x_1=1,y_1=2,\alpha ={60}^{\circ },m=-1$$

So, the equations of the required sides are

$$y-2=\frac{-1+\tan {60}^{\circ }}{1+\tan {60}^{\circ }}(x-1)\text{ and }y-2=\frac{-1-\tan {60}^{\circ }}{1-\tan {60}^{\circ }}(x-1)$$

$$\Rightarrow y-2=\frac{\sqrt{3}-1}{\sqrt{3}+1}(x-1)\text{ and }y-2=\frac{\sqrt{3}+1}{\sqrt{3}-1}(x-1)$$

$$\Rightarrow y-2=(2-\sqrt{3})(x-1)\text{ and }y-2=(2+\sqrt{3})(x-1)$$

Solving x + y = 0 and $$y-2=(2-\sqrt{3})(x-1)$$, we get:

$$x=-\frac{\sqrt{3}+1}{2},y=\frac{\sqrt{3}+1}{2}$$

$$\therefore B\equiv (-\frac{\sqrt{3}+1}{2},\frac{\sqrt{3}+1}{2})\text{ or }C\equiv (\frac{\sqrt{3}-1}{2},-\frac{\sqrt{3}-1}{2})$$

AB = BC = AD = $$=\sqrt{6}\text{ units }$$

$$\therefore$$ Area of the required triangle = $$\frac{\sqrt{3}\times {\left(\sqrt{6}\right)}^2}{4}=\frac{3\sqrt{3}}{2}\text{ square units }$$