Advertisements
Advertisements
Question
If the side of a square is tripled, how many times the perimeter of the first square will that of the new square be?
Solution 1
Let the length of each side of the old square = s
Then, perimeter of the old square = 4 × side = 4 × s = 4s
When the length of each side of the square is tripled, then
length of each side of the new square = 3s
∴ perimeter of the new square = 4 × side
= 4 × 3s
= 3 × 4s
= 3 × perimeter of the old square ...[∵ perimeter of the old square = 4s]
Hence, the perimeter of the new square will become three times the perimeter of the old square.
Solution 2
To determine how the perimeter of the new square compares to the original square when the side is tripled, follow these steps:
Step 1: Formula for the Perimeter of a Square
The perimeter of a square is given by:
P = 4 × Side
Step 2: Original Square
Let the side of the original square be s.
The perimeter of the original square:
Pold = 4 × s
Step 3: New Square (Tripled Side)
If the side of the square is tripled, the new side becomes 3s3s3s.
The perimeter of the new square:
Pnew = 4 × (3s) = 12 × s
Step 4: Compare Perimeters
The ratio of the new perimeter to the old perimeter is:
`(P_"new")/(P_"old") = (12xxs)/(4xxs) = 3`
The perimeter of the new square will be 3 times the perimeter of the original square.
RELATED QUESTIONS
What is the value of a rectangular plot of land 75.5 m long and 30.5 m broad at the rate of 1000 rupees per square metre?
If the cost of 1 sq m of a plot of land is 900 rupees, find the total cost of a plot of land that is 25 m long and 20 m broad.
Is this shape half of the big rectangle?

Hmmm...... So its area is ______ square cm.
Find the area of the rectangle whose sides are:
2 km and 3 km
By splitting the following figure into rectangles, find their areas (The measures are given in centimetres).
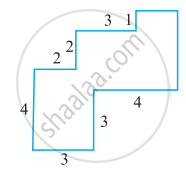
By splitting the following figure into rectangles, find their areas (The measures are given in centimetres).
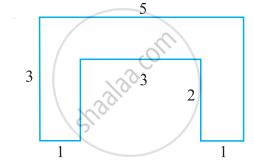
Split the following shape into rectangle and find their area. (The measures are given in centimetres).
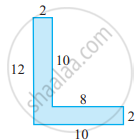
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are:
70 cm and 36 cm
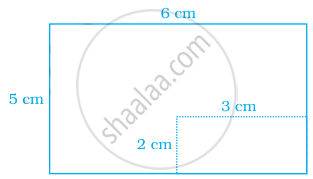
A rectangular piece of dimensions 3 cm × 2 cm was cut from a rectangular sheet of paper of dimensions 6 cm × 5 cm (see the figure). Area of remaining sheet of paper is ______.
The dimensions of a plot are 200 m × 150 m. A builder builds 3 roads which are 3 m wide along the length on either side and one in the middle. On either side of the middle road he builds houses to sell. How much area did he get for building the houses?
