Advertisements
Advertisements
Question
By splitting the following figure into rectangles, find their areas (The measures are given in centimetres).
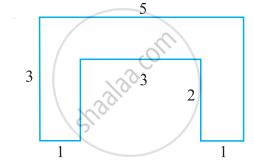
Solution
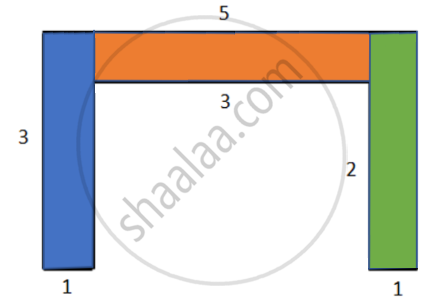
Area of brown region = 3 × 1
= 3 cm2
Area of orange region = 3 × 1
= 3 cm2
Area of grey region = 3 × 1
= 3 cm2
Total area = 3 + 3 + 3
= 9 cm2
∴ The total area is 9 cm2.
APPEARS IN
RELATED QUESTIONS
If the length and breadth of a rectangle are doubled, how many times the perimeter of the old rectangle will that of the new rectangle be?
If the side of a square is tripled, how many times will its area be as compared to the area of the original square?
The area of a rectangular garden of length 40 m, is 1000 sqm. Find the breadth of the garden and its perimeter. The garden is to be enclosed by 3 rounds of fencing, leaving an entrance of 4 m. Find the cost of fencing the garden at a rate of 250 rupees per metre.
What will be the labour cost of laying the floor of an assembly hall that is 16 m long and 12 m wide if the cost of laying 1 sq m is 80 rupees?
Find the area of the following rectangle
length = 7 m and breadth = 4 m
Find the area of the rectangle whose sides are:
3 cm and 4 cm
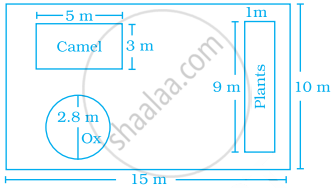
People of Khejadli village take good care of plants, trees and animals. They say that plants and animals can survive without us, but we can not survive without them. Inspired by her elders Amrita marked some land for her pets (camel and ox) and plants. Find the ratio of the areas kept for animals and plants to the living area.
A carpet of size 5 m × 2 m has 25 cm wide red border. The inner part of the carpet is blue in colour (see the figure). Find the area of blue portion. What is the ratio of areas of red portion to blue portion?

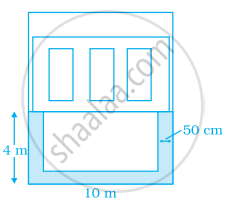
A 10 m long and 4 m wide rectangular lawn is in front of a house. Along its three sides a 50 cm wide flower bed is there as shown in the given figure. Find the area of the remaining portion.
4 squares each of side 10 cm have been cut from each corner of a rectangular sheet of paper of size 100 cm × 80 cm. From the remaining piece of paper, an isosceles right triangle is removed whose equal sides are each of 10 cm length. Find the area of the remaining part of the paper.
