Advertisements
Advertisements
Question
If the side of a square is tripled, how many times will its area be as compared to the area of the original square?
Solution
Let the length of each side of the original square = s
Area of original square = side × side = s2
When the side of the square is tripled, then length of each side of new square is 3s
Area of new square = side × side
= 3s × 3s
= 9s2
= 9 × s2
= 9 × area of original square ... [∵ area of original square = s2]
Hence, the area of the new square will become nine times the area of the original square.
RELATED QUESTIONS
As shown in the figure, four napkins, all of the same size, were made from a square piece of cloth of length 1 m. What length of lace will be required to trim all four sides of all the napkins?

The area of a rectangle is 102 sqcm. If its length is 17 cm, what is its perimeter?
Find the area of the following rectangle
length = 7 m and breadth = 4 m
Here is a rectangle of an area of 20 square cm.

Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?
If length of a rectangle is halved and breadth is doubled then the area of the rectangle obtained remains same.
Perimeter of a square and a rectangle is same. If a side of the square is 15 cm and one side of the rectangle is 18 cm, find the area of the rectangle.
Split the following shape into rectangle and find their area. (The measures are given in centimetres)

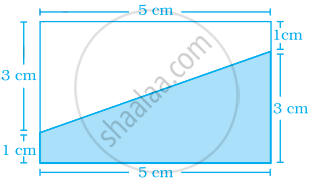
Area of shaded portion in the figure given below is ______.
The dimensions of a plot are 200 m × 150 m. A builder builds 3 roads which are 3 m wide along the length on either side and one in the middle. On either side of the middle road he builds houses to sell. How much area did he get for building the houses?
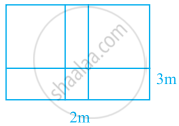
A school playground is divided by a 2 m wide path which is parallel to the width of the playground, and a 3 m wide path which is parallel to the length of the ground in the given figure. If the length and width of the playground are 120 m and 80 m respectively, find the area of the remaining playground.