Advertisements
Advertisements
Question
In Δ ABC and Δ PQR,
∠ ABC ≅ ∠ PQR, seg BD and
seg QS are angle bisector.
`If (l(AD))/(l(PS)) = (l(DC))/(l(SR))`
Prove that : Δ ABC ∼ Δ PQR

Solution
Proof : `(l(AD))/(l(PS)) = (l(DC))/(l(SR))` ∴ `(l(AD))/(l(DC)) = (l(PS))/(l(SR))`
According to angle bisector theorem, `(l(AD))/(l(DC)) = (l(AB))/(l(BC)) ; (l(PS))/(l(SR)) = (l(PQ))/((QR))`
`∴ (l(AB))/(l(BC)) = (l(PQ))/(l(QR))` and ∠ ABC ≅ ∠ PQR ..... (Given)
Δ ABC ∼ Δ PQR ........ (SAS Test)
APPEARS IN
RELATED QUESTIONS
Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

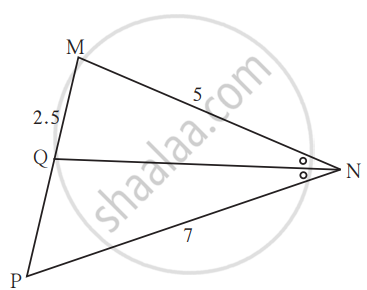
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7 MQ = 2.5 then find QP.
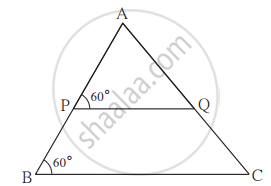
Measures of some angles in the figure are given. Prove that `"AP"/"PB" = "AQ"/"QC"`.
Find QP using given information in the figure.

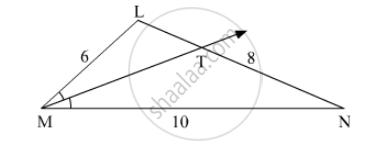
In ∆LMN, ray MT bisects ∠LMN If LM = 6, MN = 10, TN = 8, then Find LT.
In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.

Complete the proof by filling in the boxes.
In △PMQ, ray MX is bisector of ∠PMQ.
∴ `square/square = square/square` .......... (I) theorem of angle bisector.
In △PMR, ray MY is bisector of ∠PMQ.
∴ `square/square = square/square` .......... (II) theorem of angle bisector.
But `(MP)/(MQ) = (MP)/(MR)` .......... M is the midpoint QR, hence MQ = MR.
∴ `(PX)/(XQ) = (PY)/(YR)`
∴ XY || QR .......... converse of basic proportionality theorem.
In the given fig, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y. AB = 5, AC = 4, BC = 6 then find `"AX"/"XY"`.


In ΔABC, ray BD bisects ∠ABC.
If A – D – C, A – E – B and seg ED || side BC, then prove that:
`("AB")/("BC") = ("AE")/("EB")`
Proof :
In ΔABC, ray BD bisects ∠ABC.
∴ `("AB")/("BC") = (......)/(......)` ......(i) (By angle bisector theorem)
In ΔABC, seg DE || side BC
∴ `("AE")/("EB") = ("AD")/("DC")` ....(ii) `square`
∴ `("AB")/square = square/("EB")` [from (i) and (ii)]
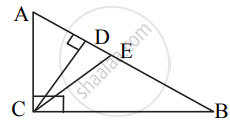
In ΔABC, ∠ACB = 90°. seg CD ⊥ side AB and seg CE is angle bisector of ∠ACB.
Prove that: `(AD)/(BD) = (AE^2)/(BE^2)`.
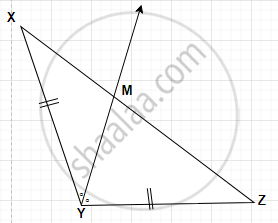
In the figure, ray YM is the bisector of ∠XYZ, where seg XY ≅ seg YZ, find the relation between XM and MZ.
Draw seg AB = 6.8 cm and draw perpendicular bisector of it.
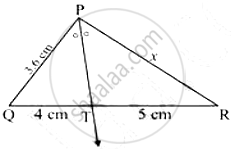
In the following figure, ray PT is the bisector of ∠QPR Find the value of x and perimeter of ∠QPR.
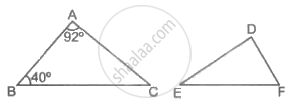
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
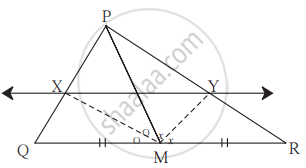
In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.
Complete the proof by filling in the boxes.
solution:
In ∆PMQ,
Ray MX is the bisector of ∠PMQ.
∴ `("MP")/("MQ") = square/square` .............(I) [Theorem of angle bisector]
Similarly, in ∆PMR, Ray MY is the bisector of ∠PMR.
∴ `("MP")/("MR") = square/square` .............(II) [Theorem of angle bisector]
But `("MP")/("MQ") = ("MP")/("MR")` .............(III) [As M is the midpoint of QR.]
Hence MQ = MR
∴ `("PX")/square = square/("YR")` .............[From (I), (II) and (III)]
∴ XY || QR .............[Converse of basic proportionality theorem]
