Advertisements
Advertisements
Question
In Fig. 14.46, the area of ΔABC (in square units) is

Options
15
10
7.5
2.5
Solution
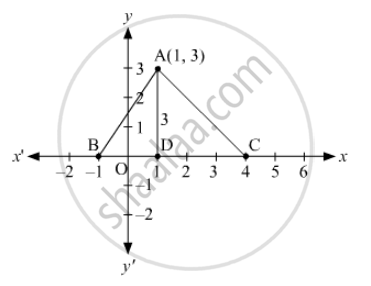
The coordinates of A are (1, 3).
∴ Distance of A from the x-axis, AD = y-coordinate of A = 3 units
The number of units between B and C on the x-axis are 5.
∴ BC = 5 units
Now,
Area of ∆ABC = \[\frac{1}{2} \times BC \times AD = \frac{1}{2} \times 5 \times 3 = \frac{15}{2} = 7 . 5\] square units
Thus, the area of ∆ABC is 7.5 square units.
APPEARS IN
RELATED QUESTIONS
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when The centre of the square is at the origin and coordinate axes are parallel to the sides AB and AD respectively.
Prove that the points (3, 0), (4, 5), (-1, 4) and (-2, -1), taken in order, form a rhombus.
Also, find its area.
Prove that the points (4, 5) (7, 6), (6, 3) (3, 2) are the vertices of a parallelogram. Is it a rectangle.
Determine the ratio in which the point (-6, a) divides the join of A (-3, 1) and B (-8, 9). Also, find the value of a.
Show that the points A(3,0), B(4,5), C(-1,4) and D(-2,-1) are the vertices of a rhombus. Find its area.
Show that the points A(2,1), B(5,2), C(6,4) and D(3,3) are the angular points of a parallelogram. Is this figure a rectangle?
The line segment joining A( 2,9) and B(6,3) is a diameter of a circle with center C. Find the coordinates of C
The measure of the angle between the coordinate axes is
If (a,b) is the mid-point of the line segment joining the points A (10, - 6) , B (k,4) and a - 2b = 18 , find the value of k and the distance AB.
If the distance between points (x, 0) and (0, 3) is 5, what are the values of x?
If P (2, 6) is the mid-point of the line segment joining A(6, 5) and B(4, y), find y.
If the points A (1,2) , O (0,0) and C (a,b) are collinear , then find a : b.
If three points (0, 0), \[\left( 3, \sqrt{3} \right)\] and (3, λ) form an equilateral triangle, then λ =
If P is a point on x-axis such that its distance from the origin is 3 units, then the coordinates of a point Q on OY such that OP = OQ, are
If the perpendicular distance of a point P from the x-axis is 5 units and the foot of the perpendicular lies on the negative direction of x-axis, then the point P has ______.
The points whose abscissa and ordinate have different signs will lie in ______.
The coordinates of two points are P(4, 5) and Q(–1, 6). Find the difference between their abscissas.
In which ratio the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4)?
Statement A (Assertion): If the coordinates of the mid-points of the sides AB and AC of ∆ABC are D(3, 5) and E(–3, –3) respectively, then BC = 20 units.
Statement R (Reason): The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.
