Advertisements
Advertisements
प्रश्न
In Fig. 14.46, the area of ΔABC (in square units) is

विकल्प
15
10
7.5
2.5
उत्तर
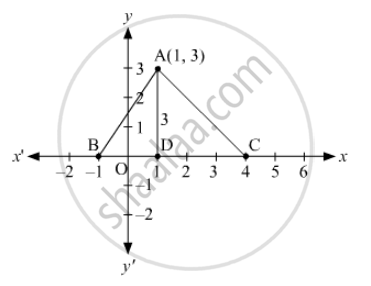
The coordinates of A are (1, 3).
∴ Distance of A from the x-axis, AD = y-coordinate of A = 3 units
The number of units between B and C on the x-axis are 5.
∴ BC = 5 units
Now,
Area of ∆ABC = \[\frac{1}{2} \times BC \times AD = \frac{1}{2} \times 5 \times 3 = \frac{15}{2} = 7 . 5\] square units
Thus, the area of ∆ABC is 7.5 square units.
APPEARS IN
संबंधित प्रश्न
The three vertices of a parallelogram are (3, 4) (3, 8) and (9, 8). Find the fourth vertex.
If two opposite vertices of a square are (5, 4) and (1, −6), find the coordinates of its remaining two vertices.
If (−2, 3), (4, −3) and (4, 5) are the mid-points of the sides of a triangle, find the coordinates of its centroid.
Name the quadrilateral formed, if any, by the following points, and given reasons for your answers:
A(-1,-2) B(1, 0), C (-1, 2), D(-3, 0)
Find the points of trisection of the line segment joining the points:
(3, -2) and (-3, -4)
In what ratio is the line segment joining the points (-2,-3) and (3, 7) divided by the y-axis? Also, find the coordinates of the point of division.
Determine the ratio in which the point (-6, a) divides the join of A (-3, 1) and B (-8, 9). Also, find the value of a.
The line segment joining the points A(3,−4) and B(1,2) is trisected at the points P(p,−2) and Q `(5/3,q)`. Find the values of p and q.
Prove that the diagonals of a rectangle ABCD with vertices A(2,-1), B(5,-1) C(5,6) and D(2,6) are equal and bisect each other
The abscissa and ordinate of the origin are
Prove hat the points A (2, 3) B(−2,2) C(−1,−2), and D(3, −1) are the vertices of a square ABCD.
If (x, y) be on the line joining the two points (1, −3) and (−4, 2) , prove that x + y + 2= 0.
Write the formula for the area of the triangle having its vertices at (x1, y1), (x2, y2) and (x3, y3).
If A (1, 2) B (4, 3) and C (6, 6) are the three vertices of a parallelogram ABCD, find the coordinates of fourth vertex D.
The distance between the points (a cos 25°, 0) and (0, a cos 65°) is
If A (5, 3), B (11, −5) and P (12, y) are the vertices of a right triangle right angled at P, then y=
Find the point on the y-axis which is equidistant from the points (S, - 2) and (- 3, 2).
Point (0, –7) lies ______.
The point at which the two coordinate axes meet is called the ______.
